Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 [ 140 ] 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182

Рис. 8.14. Эпюры распределения усилия, действующего на сферичную частицу различной крупности по сечению потока и смещающего ее к центру

Вывод о том, что сферичная частица всегда движется в центре вертикального потока [см. уравнения (8.16) и (8.18)] хорошо согласуется с экспериментальными данными А.Е. Смолдырева, проводившего скоростную киносъемку движения сферичных шариков в вертикальном потоке. Итак, при закачке в скважину частиц сферичной формы (согласно второму варианту) пробкообразования наблюдаться не будет.

На практике обеспечить снабжение гравием только идеально сферичной формы невозможно. Известны классификации гравийных частиц по форме. Типичные формы гравийных частиц определяются коэффициентами окатанности и сферичности (рис. 8.15).

При движении частицы неправильной формы возникает сложное обтекание жидкости по контуру частицы, определяющееся не наличием градиента скорости по сечению потока (первая составляющая силы Жуковского), а формой частицы. Циркуляция жидкости по контуру гравийной частицы, вызванная ее неправильной формой, приводит к возникновению дополнитель-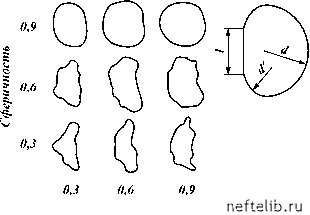

Окатанность Рис. 8.15. Типовые формы частиц

ного усилия, действующего на частицу в горизонтальной плоскости, которое было названо второй составляющей силы Жуковского. Вторая составляющая силы Жуковского может быть определена из выражения

Fж2 =P ui rot uidS.

(8.19)

Форма гравийных частиц (см. рис. 8.15) при обтекании жидкостью хорошо описывается тремя параметрами: большим d и малым d радиусами обтекания частицы и длиной вытянутой части частицы /. Из энергетической теории гидротранспорта следует, что частица гравия в потоке движется как и жидкость в водоносном пласте - по пути наименьшего сопротивления. Для гравийной частицы это означает, что в процессе транспортировки она ориентируется в потоке таким образом, чтобы сопротивление обтеканию было минимальным. Если принять во внимание, что сила сопротивления пропорциональна площади сечения частицы, перпендикулярного направлению потока, то можно предположить, что частица располагается вытянутой стороной вдоль оси потока и поэтому на циркуляцию жидкости вдоль контура частицы влияет только большой и малый радиус обтекания. Обозначим отношение d/d коэффициентом формы гравийных частиц K. Решая уравнение (8.19) с учетом принятого коэффициента формы гравийных частиц, получаем выражение для определения второй составляющей силы Жуковского

A S2

(8.20)

Вторая составляющая силы Жуковского способствует смещению частицы к границам потока. С учетом влияния формы на горизонтальное перемещение частиц в потоке дифференциальное уравнение движения частицы (8.12) при установившемся режиме запишется в следующем виде:

для случая засыпки в восходящем потоке жидкости

4-(mvx) = 2,35 pSQ22 2 [7,08(1 - K)(1 - 4x

4( X + 0,5d)

(X - 0,5Kd)

+ [pv So;2 dv, ); (8.21)

для случая засыпки в нисходящем потоке жидкости

d (mvx) = 10,527pQ2 [1,57(1 -K)

4 X A S 2

1-4(X+0,5d)22

1- AS2

4(x - 0,5Kd)

SvX: dvx ), (8.22)

где Ц - вязкость жидкости.

Выражения (8.21) и (8.22) представляют собой нелинейные дифференциальные уравнения второго порядка, которые не решаются обычными методами интегрирования. При анализе условий формирования первичных структур гравийных пробок за счет смещения частиц из центральных в периферийные сечения потока первостепенное значение приобретает оценка установившегося движения частиц, для которого справедливы граничные условия

(mVx) = 0; = 0.

С учетом принятых граничных условий решение уравнений (8.21) и (8.22) показывает, что при различных коэффициентах формы частицы гравия будут стремиться занять строго определенное положение в потоке. Если форма частицы правильная и K = 1, то частица гравия будет двигаться в ламинарном потоке жидкости в центре потока. Если K уменьшается, то частица гравия будет смещаться от центра к границам потока. С целью