Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 [ 15 ] 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68

общих приближенных методов в теории фильтрации является метод интегральных соотношений [3].

Сущность его заключается в том, что исходное дифференциальное уравнение (11.86 ) или (11.98) в области возмущения скважины заменяется системой интегральных соотношений вида

fdpldtfiix, t)dx = xf%p/dxfi(x, t)dx, г = 0, 1, п, (11.118)

где fi{x, t), i = О, I, . . ., п образуют полную систему как функции от X на отрезке [L\{t), L2{t)]. Если р{х, t), представить в виде разложения в ряд по функциям fi{x, t), то из (11.118) получим систему уравнений для коэффициентов этого ряда.

Рассмотрим задачу о возмущении первоначального стационарного движения в пласте. Возьмем простейшую систему функций - последовательные степени пространственной переменной

IjA, А, Aj ...

Пусть в момент / = О происходит отбор жидкости из пласта с расходом - kbhHG. Давление в этом случае распределено по линейному закону

р{х, ЩР + Gx. (11.119)

Будем искать приближенное решение задачи в виде многочлена

р{х, t) = Po{t) + Pi{t)x/l+, +Pn{t)x4l (0<х<1),

р{х, t)p{x, 0) {х>1). (П. 120)

В таком виде задача имеет л-f 2 неизвестных: Pi{i) и l{t). Для их определения можно составить систему уравнений, состоящую из некоторого числа интегральных соотношений, граничного условия при х = 0 н условия при X = I. При х - 1 должны выполняться условия непрерывности давления р {I, t) == Р -\- GI н некоторой степени гладкости функции р{х, t):

dp (l, t)ldx = др {I, t)/dx = ... = aV (/, tydx" = 0.

Выбор наилучшего приближенного метода расчета р {х, t) связан с тем, насколько удачно подобрано число используемы.х интегральных соотношений и условий гладкости.

В рассматриваемом случае

р{0, t) = pu р(х, 0) = уРо = 0. (П. 121)

Используя интегрирование по частям и теорему о дифференцировании определенного интеграла, приведем систему (11.118) к виду

/pxdx = yp{0, t), (11.123) b

1 J рхЧх %k{k-\)\ рх-Чх, k>2. (П. 124)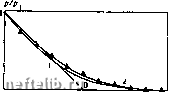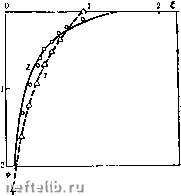

РИС. 6. к задаче о нестационарном притоке к галерее:

о - нулевое приближение; 1 - первое приближение; 2 - точное решение

РИС. 7. Зависимость безразмерного давления от безразмерной координаты для осеснм-метричного течения. Решения: / - приближенное; 2 - точное

При л = 1 из (П.122) следует

/ = 2 yVt, и (О, t) = -kidp/dx)!i>. = k(pi- po)/2i V. (II. 125) Напомним, что при точном решении по формуле (11.93) получим

«о (О, t) = k{pi-po)/\>.V(- (11.126)

Заметим, что решение для п - 1 совпадает с тем, которое получается по известному методу последовательной смены стационарных состояний [44].

Для второго приближения (п = 2) используем снова соотношение (11.122) и условие

{др/дх)ы-о = 0, (11.127>

что дает

р{х, t) = pi{\-xJlf, /2=12х/. (11.128)

Для скорости фильтрации при л; = О получим

и (О, t) = k (pi - poVVSt, (П. 129)

что близко к точному решению (11.126). Если во втором приближении вместо (11.127) использовать интегральное соотношение (11.122), то вид решения не изменится.

Если для третьего приближения (л = 3) использовать соотношения (11.122), (11.123) и (11.127), то третье приближение совпадает со вторым. Если же использовать первые три интегральных соотношения без условия (11.127), то получим (опуская промежуточные выкладки)

/7(л;, 0 = 0,583C-f0,107C2-f0,0061C3), : = х/У. (11.130)

На рис. 6 приведено сопоставление полученных приближенных решений с точными. При построении приближений более высокого порядка возникают трудности, обусловленные тем, что отсутствуют сколько-нибудь обоснованные правила выбора

наилучшего из нескольких дополнительных условий. Кроме того, при этом приходится строить приближения функций с помощью многочленов высокого порядка. Впрочем, основная цель построения приближенных решений - получение простых аналитических зависимостей- достигается уже приближениями второго порядка.

Рассмотрим без подробных выкладок осесимметричную задачу о пуске скважин с заданным дебитом q в бесконечном пласте. Решение уравнения (11.98) ищется в виде

р{г, t) = q\nir/l) + Po + Piir/l)+, +Рп{гПГ, (11.131)

где l{f) - переменный радиус зоны возмущения. Система интегральных соотношений имеет вид

"(•%(г, t)dr=-,q, (11.132)

d (О т

Iri+pir, t)dr==y,k lp{r, t)r<-4r (k>l). (11.133) b b

В нулевом приближении (Pq = -Pi = ... =0) имеем единственную неизвестную функцию l{t), которая определяется из уравнения (11.132):

/ = 2]/х/, ро{г, 0 = <7ln(r/2]/xO- (11.134)

С использованием уравнений (11.132), (11.133) и условий непрерывности р и др/дг (т. е. р = 0 и др/дг = 0) при r=l{t) получим первое приближение в виде

l = y\2t, p = q\n{r/VT2t)-q + qr/ymt. (11.135)

При сопоставлении приближенных решений 1 с точным 2 (рис. 7) имеем, что даже результаты расчета по формуле (11.134) и тем более по формуле (11.135) довольно хорошо согласуются с точным решением.

Метод интегральных соотношений позволяет с удовлетворительной точностью получить простые приближенные решения задач о притоке к скважинам в ограниченном пласте. Соответствующие точные решения получаются в виде плохо сходящихся рядов Фурье - Бесселя и трудно обозримы. Ограничимся здесь одним примером.

Рассмотрим круговой пласт радиуса R, на контуре которого поддерживается постоянное давление, равное начальному (принимаемому за нуль). В начальный момент производится пуск скважины пренебрежимо малого радиуса, расположенной в центре пласта. Тогда вплоть до момента t = ti = R/I2%t в первом приближении справедливо представление (11.135). При t>ti необходимо учитывать условие на контуре

piR, 0 = 0. (11.136)

Используя снова первое приближение разложения (11.131) п полагая l{t) = R, получим с учетом (11.136)

р(г, t} = qln{r/R) + PQ{t}{l-r/R). (11.137)