Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 [ 23 ] 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68

Заметим теперь, что в реальных задачах задается поток газа через скважину, хотя и малого, но конечного фиксированного радиуса, так что граничное условие на скважине имеет вид (П. 206).

Покажем, что построенное выше автомодельное решение удовлетворяет с большой степенью точности этому условию уже спустя несколько секунд после начала процесса.

В самом деле, на основании (П. 208) имеем

Однако из сказанного выше следует, что при малых X значение функции \dF\ld\ близко к-X при всех I, не превосходящих нескольких десятых.

При радиусе скважины R\(i см, проницаемости k= 10-2 ч", пористости mss0,2, вязкости (i ===0,01 мПа-с величина а?Р = = kP/2mi>. имеет порядок 10-10 см/с, и тогда уже при = 3 с

$ = /?(а2Р/)-/2<0,2.

Поэтому можно с весьма высокой степенью точности полагать при > 3 с

(W/=?/dOE=«(aP <)-/2 = - X.

Используя это обстоятельство, в соотношении (П. 224) получаем, что спустя несколько секунд после начала движения автомодельное решение с большой степенью точности удовлетворяет граничному условию (П. 207).

Как было показано, встречающиеся на практике значения параметра X. по модулю значительно меньше, чем рассмотренное только что, примерно равное - 0,08. Поэтому для меньших X, это условие будет удовлетворяться еще быстрее.

Выше было отмечено, что автомодельные решения при X < О соответствуют отбору газа из пласта через расширяющуюся со временем скважину. Покажем теперь, что это неестественное, на первый взгляд, свойство решений не препятствует применению их к реальным задачам, поскольку для представляющего практический интерес времени расширяющаяся (фиктивная) скважина всегда остается внутри настоящей скважины. Для этого определим поря-рядок величины f(X) - координаты точек подхода кривой Fi{, X) при Х<0 к оси абсцисс. Как было отмечено, при т.е., в

частности, при $=У(Х), функция fi ($, X) с высокой степенью точности удовлетворяет соотношению

/?($, >-)-/=1(1, Х) = -Х1п ($/$.). Полагая $ =F(X), f i ($, X) = О, получаем

fUK >.) = >-In (Г/U; !(>.) = $. ехр [x-f?($., X) . При X К 0,08, Fl ($., X) = 0,72, X < О значение $. = 0,0050, откуда $ (X) 0,005 е-б-5 = 0,75 • 10-5. j показывает формула

(11.214), промежуток времени Т, за который расширяющаяся внутренняя скважина достигает размера настоящей сксажины, составляет

Г = ? (аТ2Я)-.

С учетом предыдущих сценок для Г, аР и R получим примерно Т 10 с - около шести лет. Отметим, что значение X = 0,08 очень велико сравнительно со значениями, встречающимися на практике. При уменьшении X величина Т резко возрастает: так, при Х = 0,01 Т=\<У лет. Таким образом, для реальных задач расширяющаяся (фиктивная) скважина всегда остается внутри настоящей.

Приведенные оценки показывают, что рассматриваемое автомодельное решение вполне пригодно для реальных задач.

Автомодельность расматриваемой задачи была отмечена Л. С. Лейбензоном и П. Я. Полубариновой-Кочиной. Изложенное решение этой задачи дано Г. И. Баренблаттом.

Задача 1. Пусть проницаемссть и пористость пористой среды, плотность и вязкость газа - функции давления. Вводя функцию

jdp, (П.225)

называемую функцией Лейбензона, привести уравнение движения газа к виду

dPIdt = х(Р)1Р. (П. 226)

Показать, что прн обычных значениях дебитов динамику изменения давления в газовой скважине можно описать, заменяя переменный коэффициент в правой чьсти уравнения х (Р) постоянным хо = * (о) отвечающим начальному значению давления (линеаризация по Л. С. Лейбснзону).

Задача 2. В большинстве случаев зависимости параметров пористой среды и газа (жидкости) от давления с достаточной точностью могут быть приближены экспоненциальными функциями ( = oe°* т = mtniP) и т. д. Показать, что уравнение для давления в этом случае эквивалентно уравнению политропической фнль грации газа

ар/а/= aVp""*"• (11.227)

Задача 3. Используя методы, изложенные в §§ 4 и 5 данной главы, найтя способы определения параметров пласта по кривым изменения давления в газовых скважинах.

Задача 4. Рассмотрим уравнение (11.227) для радиально-симметричного движения. Допустим, что начальное давление в пласте пренебрежимо мало, а в начальный момент в скважину быстро закачивается конечное количество жидкости М («мгнованный источник»), так что искомое решение удовлетворяет ус-лови ям

р {г, 0) = о, ( р {г, t) rdr = Mq. (П.228>

Показать, что движение автомодельно и соответствующее ему распределение давления дается соотношением

р - pfi (£); е = .3/93/4 ; Р =

/ Mq \1/2

/, = (/2 - 2)/,2; о< £ < / = 8; /, =0, е > Л (П.229)

Дать обобщение этой постановки и результата на прямолинейно-параллельное и сфернческн-симметричное движения.

глава

НЕКЛАССИЧЕСКИЕ МОДЕЛИ ДВИЖЕНИЯ ОДНОРОДНЫХ ЖИДКОСТЕЙ

§ 1. Теория фильтрации неньютоновских жидкостей. Закон фильтрации

Неньютоновские жидкости. Аномальными или неньютоновскими называются жидкости, не следующие классической модели вязкой жидкости [35]. Наиболее простые из них нелинейно-вязкие жидкости, для которых девиатор тензора напряжений однозначно определяется девиатором тензора скоростей деформаций, они соосны, но зависимость между ними нелинейна. При простом сдвиге это проявляется в нелинейности кривой течения, связывающей касательное напряжение т и скорость сдвига f (рис. 17):

x = f(T); т=Г(). (HI.1)

Нас будут прежде всего интересовать структурирующиеся нелинейно-вязкие жидкости, способные образовывать твердообразные структуры, разрушающиеся при увеличении интенсивности деформации. Такие жидкости являются псевдопластическими: кривая ч = Т(х) для них выпукла к оси х: Г"(х)>0. Крайнее проявление псевдопластичности описывается известной моделью

, „ вязко-пластнческой жидкос-

РИС. 17. Кривые течения ньютоновской (а), псевдопластической (б), дилатантной (в) и бингамовской (г) жидкостей

ти, определяемой соотношениями Бингама - Шведова: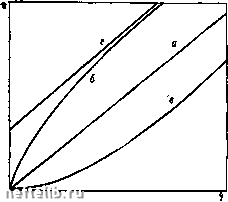

Т = -q- (х - хр), X > Хо, 7 = 0, О < X < Хо.

(1П.2)

Здесь То - предельное напряжение сдвига; г\ - структурная вязкость.

Для описания экспериментальных данных, особенно в небольшом диапазоне изменения переменных, часто используется и степенная зависимость вида

X = К". (1П.З)