Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 [ 64 ] 65 66 67 68

РИС. 64. К задаче о вы-теснении иефти оторочкой активной прнмеси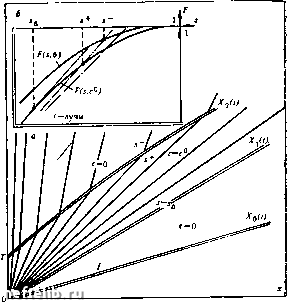

t = Т на границе х = 0 появляется скачок концентрации. При t >Т распространяющееся от него возмущение взаимодействует с центрированной волной, примыкающей в автомодельном решении ко входу пласта. Ограничимся простейшим вариантом задачи, когда изотермы сорбции а (с) и распределения примеси <р (с) линейны:

а = тТс, f = foc. (V.79>

В этом случае, как легко установить, прямой и обратный скачки концентрации распространяются без искажения; мгновенная, скорость скачка в каждый момент

и f± + yo/(l-yo)

S+-S- т s± + (<po+r)/-(l-<po)

Таким образом, на (s, Р)-диаграмме каждому сопряженному s, с скачку соответствует, как и в автомодельном решении, переход по лучу, проходящему через полюс (-Sp, -Fp), с одной из кривых F{s, 0), F (S, с") на другую.

Проведем на плоскости {х, t) траектории скачков: Хо (t) - переднего скачка насыщенности; Xi{t) и Хг (О - переднего и заднего сопряженных скачков насыщенности и концентрации (рис. 64). Рассмотрим траекторию заднего скачка, распространяющегося по центрированной волне отвечающей автомодельному решению так, что Х2 = (U/m) F, s (S+, с") t, (V.81)

где S+ - насыщенность перед скачком. С другой стороны, из условий (V.80)

S++,

(V.82)

Подставляя (V.82) в (V.81), получим

/ = Г ехр

F" (s, с°) ds

f(s.cO)-[f (s, c°) + F]/(s-s)

(V.83)

Соотношение (V.83) устанавливает зависимость от времени насыщенности S+ перед вторым сопряженным скачком. Координаты и скорость скачка определяются соотношениями

Хг = (U/m) F (s+, с") t, V = (U/m) [F (s+) + f p] (s+ -f Sp)-. (V.84)

Из (V.83) и (V.84) видно, что по мере распространения второго скачка его скорость постепенно увеличивается и стремится к скорости первого сопряженного скачка f (вд); насыщенность перед фронтом постепенно убывает и стремится к при / - со; она в каждой точке меньше скорости соответствующей характеристики F(s+). Отсюда следует, что второй скачок не влияет на условия распространения первого сопряженного скачка и на решение при x>Xiii).

Расстояние между скачками равно

L (О = X, (О - Хг (О = (Ulm) t [F (s,)- F (s+)]. (V.85)

Используя (V.83), легко показать, что существует конечный предел L{oo) = L,. Таким образом, асимптотически при i-у оо формируется стационарная оторочка, движущаяся со скоростью, равной скорости первого сопряженного скачка Vi = (I m) F(вд). Чтобы построить решение в области за вторым скачком, заметим, что из последнего условия (V.80) можно найти величину s- (t) - проще всего это сделать графически (см. рис. 64). Легко видеть из рис. 64, что а скачком (л; == Х? - 0) оба семейства характеристик уходят со скачка. Поэтому решение в области л; < Х2(0 определяется полностью начальными данными на линии х = Х2 (t) и описывается уравнением

х (i, S) = Х2 (/2. S) + F (S, 0) (U/m) (t - t2 (s)). (V.S6)

Здесь в качестве параметра на линии л; = Хг (i) взята насыщенность непосредственно за скачком, s = s-; Х2 и /2 - соответствующие значения координаты скачка и времени.

Естественно поставить вопрос об асимптотике решения при больших временах. Ее можно получить, рассматривая предел полученного выше решения. Можно, однако, рассуждать и по-другому. Как было показано, со временем оторочка стабилизируется и начинает двигаться с постоянной скоростью. Поэтому будем искать в подвижной системе координат, связанной с оторочкой, стационарное решение вида

S = Si-q), C=C(7i), >i = X~Vt,

С() = 0, h>/, С(7з) = сО, <Л (V.87)

Подставляя выражения (V.87) в основную систему (V.47), получим:

~mV + U~=0, -UF + niVS = consU, у d [mcs + m О - s) у + а] d [cF-\-у\ - F)\

- [mcs-\-m{\ - s)-f a]y-f [/[cF-f <р(1 - F)] = const2.

Как нетрудно видеть, условия (V.88) показывают, что значения насыщенностей перед оторочкой s+ и за ней s- связаны между собой и со скоростью V условием на скачке:

mVlU = {F+ - F-)l{s+ - sr). (V.89)

При этом значение s внутри оторочки определяется пересечением прямой, соединяющей точки M+{s+, F+) и M~{sr-, F-) с кривой F = F(s, сО).

Второе уравнение (V.88) показывает, что прямая ММ~ проходит через полюс (-Sp, -Fp). Наконец, учитывая условия устойчивости переднего и заднего фронтов оторочки, легко убедиться, что прямая ММ~ должна быть касательной к кривой F{s, с"), чем положение этой прямой и всех элементов решения определяется однозначно. Построенное инвариантное решение типа равномерно распространяющейся волны с точки зрения задачи в целом представляет собой внутреннюю асимптотику решения, отвечающую малости объема оторочки или - что эквивалентно - большим временам наблюдения. Внешним решением задачи при этом, как легко видеть, будет решение задачи двухфазной фильтрации в отсутствие активной примеси (с = 0) с дополнительным скачком насыщенности, обусловленным наличием тонкой оторочки. Положение этого скачка определяется величинами s+ и s-, определяемыми из внутреннего решения. На (s, F)-flHarpaMMe ему соответствует путь ABGDE. Полученный результат заслуживает особого комментария. Дело, в том, что автомодельное решение задачи вытеснения нефти водой, соответствующее пути ABGDE, существует и в отсутствие активной примеси; однако оно неустойчиво. Таким образом, роль тонкой оторочки активной примеси формально сводится к стабилизации неустойчивого решения, отвечающего рис. 59, г.. При этом, очевидно, ширина оторочки имеет второстепенное значение, а главную роль играет та максимальная степень снижения подвижности воды, которая достигается в оторочке. Если активная примесь «полезная», то F,c < О, и последнее утверждение означает, что целесообразно использовать максимальные значения концентрации примеси в оторочке.

Та же техника позволяет проанализировать влияние запаздывания закачки активного агента на показатели разработки. Запаздывание достаточно часто происходит по техническим причинам. Будем считать, что пласт, первоначально однородно насыщенный нефтью,