Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 [ 12 ] 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

б) все они остаются внутри некоторого ограниченного объема фазового пространства.

В случае неавтономных уравнений хаос возможен и в системах второго порядка. Так, в некоторой области изменения параметров хаотичными могут стать колебания нелинейного осциллятора под воздействием внешней периодической силы, описываемые уравнением Г. Дюффинга (G. Duffing, 1918 г.)

(1.9)

x + Sxc + ax + bx3 = F cos cot.

Заметим, что формально неавтономное уравнение второго порядка можно записать в виде системы трех автономных уравнений. Так, (1.9) может быть переписано в виде

Sy - ax - bx + F cos z,

=c .

Это в какой-то мере объясняет возникновение хаотических движений в неавтономных системах второго порядка.

То, что периодическое возмущение может привести к случайному поведению, иллюстрирует простая механическая система, представляющая собой шарик в плоском ящике с неровным дном (рис. 1.13).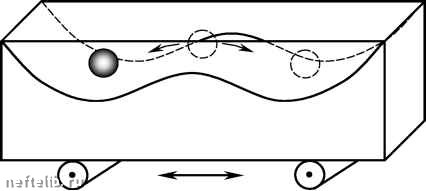

Рис. 1.13. Хаотическое движение шарика в ящике с неровным дном

Когда этот прибор покоится, шарик имеет два устойчивых и одно неустойчивое положения равновесия. Если же ящик совершает горизонтальные периодические движения достаточно большой амплитуды, то шарик начинает беспорядочно перепрыгивать из одной ямы в другую. «Разбе-гание» траекторий в этой системе связано с наличием неустойчивой точки равновесия на вершине среднего холмика.

: -bx + a

n > 1, (1.12)

dt [1 + xn (t -t)

описывающего процессы регенерации больных кровяных шариков при хронической лейкемии [20].

Примером разностного уравнения, имеющего хаотические решения, является логистическое отображение

xn+1 =mxn (1 - xn), (1.13)

введенное в 1845 г. П. Ф. Ферхюльстом для описания динамики популяций в закрытой среде (xn - относительная численность особей популяции в n-й

год). Линейный член в правой части (1.13) описывает рост или рождение,

Если рассматривать уравнения с отклоняющимся аргументом, то хаотические решения могут иметь место и в случае более простых систем - обыкновенных дифференциальных уравнений первого порядка

= f (x, x(t-t)) (1.10)

и даже алгебраических уравнений

x = f (x(t), x(t -t))

где xn = x(nt), n = 0, 1, 2,..., t> 0 - временная задержка (лаг).

Введение отклоняющегося аргумента в дифференциальные уравнения позволяет уменьшить их размерность и тем самым избежать трудностей при идентификации математических моделей, содержащих ненаблюдаемые (т. е. не измеряемые напрямую) физические переменные (см. также раздел 3.1). Следовательно, уравнения с отклоняющимися аргументами являются образами некоторых систем более высокой размерности, наподобие двумерных теней от объемных предметов на стенах пещеры Платона. Поэтому неудивительно, что в случае дифференциально-разностных и разностных уравнений хаос может проявиться и в системах, порядок которых меньше не только трех, но и двух.

Вспомним также о том, что порядок обыкновенного дифференциального уравнения совпадает с числом начальных условий, необходимых для однозначного определения его решения. Поскольку постановка начальной задачи для уравнения (1.10) требует задания значений x на всем интервале, содержащем бесконечно большое число точек, то порядок уравнения с отклоняющимся аргументом можно считать (по этому критерию) бесконечно большим. Это является еще одним объяснением возможности возникновения хаоса в системах с запаздыванием.

В качестве примера уравнения вида (1.10), допускающего хаотические решения, приведем уравнение Маки-Гласса (M. C. Mackey, L. Glass, 1977 г.)

x(t - t)

а нелинейный член ответственен за ограничение роста, связанное с недостатком энергетических или пищевых ресурсов (величина 1 - xn пропорциональна «свободной» части жизненного пространства).

Модель (1.13) весьма полезна для иллюстрации некоторых закономерностей перехода к хаосу, поэтому исследуем ее более подробно.

Графическое решение уравнения (1.13) может быть получено путем построения графика функции f (xn ) = xn (1 - xn) в координатах (xn, xn+1) (рис. 1.14).

Динамика системы (1.13) изобразится ломаной кривой 123456..., которая «притягивается» к точке равновесия P (рис. 1.14).

хи+1 I

0 Х0 Х1 х2

1 Xn

Рис. 1.14. Логистическое отображение

Отметим, что точки равновесия x* определяются из решения уравнения x*= f (x*) = x*(1 - x*) .

Для функции, представленной на рис. 1.14, это уравнение имеет два решения:

x*= 0 и x*= 1 - -,