Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 [ 37 ] 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

Метод структурной минимизации среднего риска

Итак, при постановке и решении задач идентификации моделей по эмпирическим данным ограниченного объема возникает проблема правильного соотнесения сложности идентифицируемой модели с количеством и уровнем погрешности имеющихся данных. Эта проблема может быть решена при помощи метода структурной минимизации среднего риска [16, 17]. Оказывается, что если на допустимом множестве решений задать структуру, то наряду с минимизацией эмпирического риска (невязки) внутри элементов структуры появляется дополнительная возможность минимизации по элементам структуры. Это позволяет найти решение, дающее более глубокий гарантированный минимум среднего риска, чем решение, доставляющее минимум эмпирического риска на всем допустимом множестве решений. По существу, метод структурной минимизации среднего риска является способом формализации давно применяемого на практике приема регуляризации за счет огрубления модели (см. также [8]).

Рассмотрим сущность этого метода на примере классической задачи восстановления функциональной зависимости y = F (X) по эмпирическим

данным, представленным в виде совокупности замеров (выборки) {xi; yi}, где yi - результат измерения y при X = Xi, i = 1, 2, ... , l, l - число замеров (объем выборки). Обращаясь к вероятностной интерпретации погрешностей в исходных данных, введем аддитивную помеху £:

yi = F (Xi) + £i,

где случайная величина £ имеет нулевое математическое ожидание Е[£] = 0 и конечную дисперсию D[£]< о. Несмотря на то, что задачи восстановления эмпирической зависимости не относят к некорректно поставленным, при ограниченном объеме выборки возникает проблема правильного соотнесения «сложности» приближающей (пробной) функции с объемом и качеством (уровнем погрешности) исходных данных. Использование излишне сложных моделей, содержащих большое число искомых параметров,

дович писал: «Положение вещей напоминает сказку Андерсена, в которой тень, отделившись от человека, начинает жить самостоятельно, делает карьеру и, наконец, заставляет самого человека служить ей» (цитата, приведенная в [15]).

Таким образом, при выборе разумной сложности математической модели необходим всесторонний анализ, принципы которого не до конца формализуемы. Как отмечается в [15], «умение правильно выбрать математическую модель находится на грани науки и искусства. Оно требует не только необходимых математических и прикладных знаний и опыта, но также вкуса и чувства соразмерности».

I (a )< Im (a )= 10 (a )Q

приводит в случае малых выборок к неустойчивости, подобной неустойчивости некорректно поставленных задач.

Предполагая, что класс функций, в котором ищется регрессия y(x), является параметрическим с параметрами a, задачу восстановления эмпирической зависимости можно свести к минимизации функционала

I (a )= \\(y - F (x, a )2 P(yx)dxdy), (2.46)

называемого функционалом среднего риска [16, 17]. Здесь P(yx) - плотность вероятности реализации значения y при заданном значении x. Как правило, вид функции P(yx) (характеризующий статистические свойства случайных ошибок) неизвестен, поэтому на практике вместо (2.46) минимизируется так называемый функционал эмпирического риска

10 (a) =1 (у1 - F; a)) , 1 i=1

построенный по случайной выборке { xi; yi}.

Показано [16, 17], что для величины функционала среднего риска могут быть получены верхние оценки вида

(2.47)

h I )

справедливые с вероятностью 1-. Величина h называется емкостью класса функций F(x, a) и определяет сложность идентифицируемой модели. В частном случае, если множество функций состоит из конечного числа N элементов F1(x, a), F2(x, a), ... , Fл(x, a), то h ~ ln N, а если рассматривается класс линейных по параметрам функций

F (x, a )= iaiPi (x), (2.48)

где {cpi (x)} - некоторая ортонормированная система функций, то h = л, т. е.

емкость класса функций (сложность модели) равна в этом случае числу искомых параметров л.

Величина - определяет относительный объем выборки. Структура h

второго сомножителя в (2.47) такова, что с ростом - величина \i -;-

h \ h I

уменьшается, стремясь к единице. Функционал эмпирического риска с

увеличением -, как правило, увеличивается. Таким образом, существует h

некоторое оптимальное значение -, при котором верхняя оценка среднего

риска (его гарантированное значение) достигает минимума. Это значе-1

ние - и определяет оптимальную сложность модели. h

При некоторых весьма общих предположениях могут быть получены точные оценки величины Q [16, 17], но они оказываются малопригодными, поскольку требуют знаний о статистических свойствах случайных ошибок £, а эта информация, как правило, отсутствует. Кроме того, строгие верхние оценки величины Q оказываются весьма завышенными и могут привести к слишком «осторожным» по отношению к увеличению сложности модели алгоритмам.

Поэтому на практике эти оценки используются лишь для того, чтобы

определить структуру критерия Q, характер его зависимости от величин -

А значения констант, входящих в выражения для Q, задаются ис-

ходя из априорных соображений или же подбираются на основе ретроспективного анализа опыта решения подобных задач.

Так, при восстановлении одномерной регрессии в классе функций (2.48) рекомендуется использовать критерий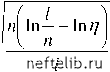

z > 0, z <0.

(2.49)

При проведении расчетов задаются некоторыми значениями п, при каждом п методом наименьших квадратов определяют параметры а, а затем вычисляют /0 (а) и по формулам (2.47)-(2.49) - функционал среднего риска /т(а).

Оптимальным признается то значение п, при котором величина /т (a) минимальна.

Пример. Обработка данных вискозиметрических исследований.

При обработке данных вискозиметрических экспериментов с реофи-зически сложными средами оценки реологических параметров часто оказываются неустойчивыми относительно малых экспериментальных ошибок. Это может быть связано, в частности, с тем, что достоверные результаты могут быть получены лишь в ограниченной области значений скорости сдвига, поскольку при слишком малых и слишком больших значениях скорости сдвига в неньютоновских средах могут иметь место явления, вносящие погрешности в измерения и искажающие истинную картину течения в рабочем зазоре ротационного прибора.