Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 [ 3 ] 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

1.1. Фракталы

Весь предшествующий опыт убеждает нас в том, что природа представляет собой реализацию простейших математически мыслимых элементов.

А. Эйнштейн

Фрактальная геометрия позволяет раскрыть неожиданную простоту построения сложных природных систем и предоставляет методы их качественного и количественного описания. Для моделирования неупорядоченных систем теория фракталов играет такую же роль, как генераторы случайных чисел - для моделирования случайных процессов. Так, синтетические фрактальные пейзажи, полученные средствами компьютерной графики, выглядят настолько правдоподобно, что большинство воспринимает их как естественные. Повсеместное распространение компьютеров и

Развитие теории самоорганизации показало, что основные особенности геометрии и динамики сложных природных объектов часто удается описать с помощью достаточно простых детерминированных моделей. Обнаружение детерминированной основы в совершенно случайных, на первый взгляд, явлениях - важнейшее достижение синергетики, позволяющее надеяться на широкую применимость ее результатов при контроле и управлении процессами в сложных системах.

Подчеркнем еще раз, что эта простота универсальна - одни и те же базовые модели описывают кооперативное поведение в системах самой различной природы. В этом проявляется самоподобность Природы - свойство, позволяющее ей наиболее «экономными» способами построить все наблюдаемое нами разнообразие объектов и явлений. Несколько упрощая, мы можем сказать, что Природа, быть может, владеет немногими простыми методами конструирования, но она искусно применяет их в различных сочетаниях на многих иерархических уровнях организации сложных систем, порождая таким образом свои самые совершенные творения.

Наиболее зримо самоподобность Природы проявляется в биологической эволюции. Известно, например, что онтогенез - индивидуальное развитие организмов - подобен (в своей шкале времени) филогенезу - развитию групп (видов, родов), к которым эти организмы принадлежат.

Множество фактов проявления самоподобности в объектах и явлениях неживой и живой природы было найдено Бенуа Б. Мандельбротом (B. B. Mandelbrot), который для обозначения этого свойства ввел понятие фрактала - структуры, состоящей из частей, которые в каком-то смысле подобны друг другу [6-9].

1.1.1. Идеальные фракталы

Примером идеального фрактала является треугольник В. Серпинско-го (W. Sierpinski), который впервые описал его в 1916 г. Этот объект может быть получен путем построения, начинающегося с равностороннего треугольника (рис. 1.1).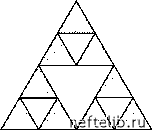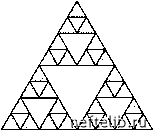

к = 1 к = 2 к = 3

Рис. 1.1. Треугольник Серпинского

На первом этапе исходный треугольник делится на 4 равносторонних треугольника, средний из которых выбрасывается. С каждым из оставшихся треугольников поступают так же. На к-м этапе мы будем иметь 3к треугольников, которые при к образуют некоторое «всюду дырявое» множество точек.

Это множество масштабно-инвариантно, поскольку увеличение в 2к любого из маленьких треугольников, полученных на к-м этапе построения, приводит к тому же самому множеству (этим свойством ковер Серпинско-го напоминает куклу-матрешку).

Еще одним примером фрактального объекта является кривая Коха, названная так в честь Хельге фон Коха, описавшего ее в 1904 г. Способ построения этой кривой ясен из рис. 1.2.

Легко уловить связь между этими структурами и примерами нигде не дифференцируемых непрерывных функций, построенных К. Вейершт-рассом (K. Weierstrass) и его последователями.

Рассмотрим, например, функцию Вейерштрасса-Мандельброта, задаваемую в виде сходящегося ряда [9]

f (x)= Z bn (1 - cos anxj

где 0 < b < 1, ab > 1.

компьютерной графики позволяет использовать фрактальные представления для исследования геометрии сложных объектов во многих областях естественных наук.

Рассмотрим некоторые математические сведения, необходимые для введения количественных мер фрактальных свойств.

k = 0

k = 1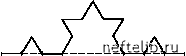

k = 2

Рис. 1.2. Кривая Коха

Легко видеть, что продифференцированный ряд

sm anx

расходится, поэтому функция не дифференцируема ни в одной точке. График этой функции представляет собой масштабно-инвариантную (т. е. фрактальную) кривую, что можно показать аналитически. Действительно,

f {ax)= tbn (l - cos an+1x)= ]Гьп+1 (l - cos an+1x)= nbn

= - f bk (1 - cosakx)= - f (x).

Отсюда следует, что если участок кривой f (x ) на отрезке

растянуть в a по оси x и в b раз по оси у, то в результате получится исходная кривая на участке [0,1]. Поскольку коэффициенты растяжения по

осям x и у не совпадают, то f (x) называют (в отличие от кривой Коха) не

самоподобной, а самоаффинной.

Нигде не дифференцируемые функции многие выдающиеся математики считали надуманными «патологическими» структурами, не имеющими никакого отношения к реальности. Так, Пуанкаре в «Науке и методе» писал: «Некогда при нахождении новых функций имелась в виду какая-нибудь практическая цель. Теперь функции изобретаются специально для того, чтобы обнаружить недостаточность рассуждений наших отцов, никакого иного вывода, кроме этого, из них нельзя извлечь». Ш. Эрмит в своем письме к Т. Стилтьесу был еще более эмоционален: «Я в ужасе отворачи-