
 |
|
|
Главная Переработка нефти и газа Теперь уже можно использовать непосредственно П-теорему подобия. Имеем П = -гН-, и=, Iln-k = - - (1.18) Окончательно получаем П = п(-5-, i, q) (1.19) Другой путь получения безразмерных параметров подобия используется в тех случаях, когда имеется математическая формулировка изучаемого явления - есть математическая модель и формулировка начальных и граничных условий. После приведения уравнений, описывающих явление, а также начальных и граничных условий к безразмерной форме получится, что в математическую формулировку входят безразмерные параметры. Если рассматривать процессы, протекающие в двух различных случаях, характеризующихся разными условиями, но так, что безразмерные параметры, входящие в уравнения, начальные и граничные условия, приведённые к безразмерной форме, остаются одними и теми же, то математическое описание процессов в двух указанных случаях будет в точности одним и тем же и, следовательно, процессы будут подобными. Конечно, математическая формулировка явления обычно оказывается возможной при его достаточно глубокой изученности. Использование методов подобия весьма плодотворно не только при экспериментальном исследовании явлений, но и при получении математических решений задач. Применение методов подобия в задачах механики подробно изложено в известной книге Л. И. Седова [102]. § 2. ОСНОВНЫЕ ПОНЯТИЯ ВЕКТОРНОГО ИСЧИСЛЕНИЯ, ТЕОРИИ ПОЛЯ И ТЕНЗОРНОГО ИСЧИСЛЕНИЯ Чтобы облегчить чтение книги, в этом параграфе кратко излагаются основы векторного и тензорного исчисления, а также теории поля. Векторами называются величины, имеющие как размеры, так и направление в пространстве. Классическими примерами векторных величин являются сила, скорость и ускорение. Давление же и температура являются примерами скалярных величин, не имеющих направления. Скалярные величины можно изображать в виде чисел. Векторные же величины изображаются отрезками, имеющими направление в пространстве. Длина вектора а называется модулем вектора и обозначается символом а или а . Два вектора а ж Ъ считаются равными только в том случае, когда равны длины векторов (модули) и совпадают их направления. Сложение и вычитание векторов производятся по правилам параллелограмма или параллелепипеда. Пусть в каждой точке пространства существует некоторая скалярная величина, например давление р. Тогда говорят, что имеется скалярное поле - поле давления. Возьмем некоторую точку О, находящуюся в начале декартовых координат х, у, z (рис. 3, а). Скалярная величина р изменяется с изменением координат, так что ,,скорость" изменения /? в направлении оси Ож будет равна производной от р = р (х, у, z) по координате х, т. е. dp/dx. Соответственно в направлениях у и z будем иметь производные dp/dy и dpidz. Единичные векторы, т. е. векторы, модули которых равны единице, направленные по осям х, у ж z (рис. 3, б), обозначаются i, / и к. Таким образом, если принять, что в направлениях х, у и z имеются векторы, модули которых равны dp/dx, dp/dy и dp/dz, то сами векторы можно обозначить соот- ветственно (dp/dx) i, (dp/dy) j и (dp/dz) к. Одной из основных характеристик поля является градиент, сокращенно обозначаемый символом grad, для которого имеем следующее выражение: 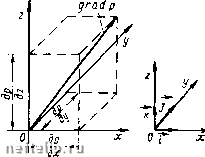 gradp = -g-7-f7+4/. Рис. 3. Градиент и его проекции на оси x, у, Z (2.1) Градиент, как видно из (2.1), ра- вен сумме векторов, направленных по осям координат, и сам является векторной величиной. Его направление для данного поля строго определенное. Производная скалярной величины по любому направлению п, не совпадающему с направлением градиента, выражается следующим образом: cos а = дх дп COS Y = dz дп (2.2) Если принять, что в направлении п имеется единичный вектор, проекции которого на соответствующие оси координат выражаются как n;c = cosa, nj, = cosP, n = cosY, (2.3) то на основе (2.2) и (2.3) получаем £- = gradp-«. (2.4) в правой части формулы (2.4) представлено скалярное произведение двух векторов grad pun. Скалярное произведение векторов, как известно, равно произведению модулей векторов на косинус утла между ними. Таким образом, производная скалярной величины р по направлению п является скалярной величиной. Чтобы несколько более подробно пояснить формулу (2.4), представим ее в развернутом виде: "Й cos (Т, Т) +1 П;. COS (/, + cos (к, Т) + + Пу cos (Т, Т) + -п, cos (7, Ъ+Пу cos {к, 7) + + -g cos ( ) +1 cos {7,к) + п, cos (X, к). (2.5) В выражениях (2.5) имеются в виду косинусы углов между соответствующими направлениями i, /, к. Поскольку косинусы углов между совпадающими линиями равны единице, а между взаимно перпендикулярными - нулю, то в правой части выражения (2.5) остаются только три члена, т. е. получаем lf-=l" + f «.+«- (2-6) Если подставить в выражение (2.6) выражения из (2.3), то и по- 4. Элемент поверхности dS лучим формулу (2.2). Рассмотрим теперь векторное поле, когда в какой-то точке пространства М (ж, у, z) имеется вектор а {М). В другой точке пространства Ml величина вектора будет иная, чем в точке М, так что в точке Ml, например, будем иметь вектор (М). Если взять некоторую произвольную поверхность 5 в векторном поле (рис. 4), то к каждому малому элементу этой поверхности будет относиться вектор а. В общем случае направления п нормали к элементу поверхности dS и вектора а, конечно, не будут совпадать. Элементарным потоком вектора df через поверхность dS называется скалярная величина df=\a\cos{n, a)dS. (2.7) Можно перпендикулярно к элементарной площадке dS направить вектор dS, модуль которого равен величине площади dS. Тогда 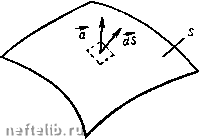 0 1 [ 2 ] 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 |
||
 |
 |