Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 [ 48 ] 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70

полном напряжении приводит к увеличению эффективного напряжения на такую же величину.

Это теоретическое положение хоропю подтверждается экспериментальными фактами. Так, разрушение покрытых непроницаемо& оболочкой образцов при различных значениях внутринорового давления р показало [50], что все экспериментальные точки на зависимости предельного эффективного напряжения а* = 5* - р, при котором происходило разрушение образца, от предельного эффективного напряжения ajj = iSj - р укладываются практически на одну прямую линию (рис. 80), как зто и следует из теории. Согдасно экспериментальным данным, показанным на рис. 80, получается, что коэффициент при давлении р равен единице.

Описанные выше эксперименты относятся к разрушению пористых образцов. Если же рассматривать результаты экспериментов по сжимаемости пористых сред, то может показаться, что соотношенио (2.3) не выполняется, так как коэффициент при давлении р в формуле (2.3) не равен единице (но результатам многих экспериментов он равен 0,85). Однако соотношение (2.3) справедливо и в этом случае. Дело в том, что норовый объем образца пористой среды зависит не только от эффективного нанряжения, но и от нейтрального напряжения, правда, не так сильно, как от эффективного напряжения.

На рис. 81 изображена в крупном масштабе пористая среда при различных значениях нейтрального нанряжения а = Pi и а = р2, Р2 > Pi) конечно, в сильно увеличенном виде.

При увеличении нейтрального напряжения от а = pi до а = р. зерна пористой среды сжимаются и уменьшается норовый объем образца этой среды, как и размеры самого образца. Хотя сжимаемость материала зерен меньше сжимаемости пористой среды от эффективных напряжений, однако она существует.

Изменение норового объема образца можно было бы измерить, поместив не покрытый оболочкой образец в бомбу высокого давления.

Допустим теперь, что измеряется изменение порового объема образца пористой среды, покрытого гибкой непроницаемой оболочкой. В этом случае норовый объем образца будет зависеть главным образом от эффективных напряжений и, в известной степени, от нейтрального нанряжения. Поэтому, используя радиально-симметрич-ную Систему координат, а также считая зависимость порового объема от напряжений в первом приближении линейной, можно написать для изменения норового объема AV/V следующую формулу:

- = Ра Да + Др = Р„ (AS - Ар) + Р„ Лр =

= Р.[Д5-Др(1-1)]; (2.4)

о=-3-, Ь--3-.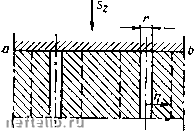

Рпс. 82. Пористая среда с узкими каналами

В формуле (2.4) - коэффициент изменения (сжимаемости) порового объема от эффективных напряжений, а Рр - коэффициент изменения порового объема от нейтрального напряжения. Пусть

Рр/Р(т = 0,15. Тогда из (2.4) имеем - AF/F = р {AS - 0,85А;г).

Приведенные выше рассуждения относятся к средам с сильно развитым поровым объемом. У пород кавернозного типа механическое взаимодействие твердого материала п насыш,аюш;их породу жидкостей происходит сложнее. Пусть согласно рис. 82 такая порода содержит жидкость лишь в вертикально расположенных «трубочках» радиусом г, со-прикасаюш;ихся с «кровлей» по контакту аЬ. Эти «трубочки» расположены далеко друг от друга, так что при изменении давления жидкости в них изменение сжатия iia-териала среды происходит практически лишь в области г < rj, прилегаюш,ей к «трубочке». Тогда изменение давления жидкости не будет вызывать в целом такого же изменения нейтрального напряжения в материале и, следовательно, приведенные выше соотношения не будут выполняться.

Однако дальнейшие рассуждения будут относиться к пористым средам с сильно развитым поровым объемом, поэтому будем основываться на полученных выше формулах. Обоб-ш;ая эти формулы, полезно представить их в тензорном виде: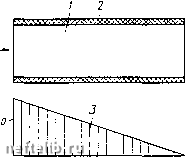

Ts = Ta + Tp, Tp = pTi, (2.5)

где Ts - тензор полного напряжения; Т(т - тензор эффективного напряжения; Tj - единичный тензор.

Взаимодействие горных пород и насыш;аюш;их их жидкостей

происходит, естественно, не только когда жидкость находится в покое, но и когда она движется. Если, например, имеем образец пористой среды в форме параллелепипеда (рис. 83), имеюш;ий снаружи непроницаемое покрытие, и к концу образца а; = О приложено

О L X

Рис. 83. Действие градиентов давления на пористую среду:

г - образец; 2 - непроницаемое покрытие; 3 - эпюра давления р; 4 - эпюра эффективного напряжения

давление жидкости р, а на другом конце образца х = I давление-жидкости равно нулю, то распределение давления жидкости в порах образца будет согласно закону Дарси представлено эпюрой 3, показанной на рис. 83. Давление жидкости в образце с ростом координаты X уменьшается, но поскольку давление жидкости создает усилие, которое должно восприниматься материалом пористой среды, в материале пористой среды должно с ростом координаты х увеличиваться эффективное напряжение cr.. Рассматривая равновесие сил в произвольном сечении образца, получаем, что распределение напряжения Од. выражается эпюрой 4, показанной на том же рис. 83, откуда видно, что

dox dp

dx dx

(2.6)

При рассмотрении взаимодействия горных пород и фильтрующейся в них жидкости также на первый взгляд получается, что поскольку фильтрующаяся жидкость занимает в осредненном единичном сечении породы часть, равную т., то как будто на элемент длины породы Ах передается усилие -тАр. Однако в среде с сильно развитым норовым объемом из-за того, что нейтральное напряжение изменяется на длине Ах на величину - (1 - т) Ар, в сумме получаем

ДсТд, = -тДр -(1 -т)Д/? = -Др. (2.7)

Конечно, соотношения (2.6) и (2.7) перестают быть справедливыми в случае сред со слабо развитым перовым объемом, таких, например, как среда, показанная на рис. 82.

Из всего сказанного выше следует, что градиенты давления фильтрующейся жидкости действуют на пористую среду как массовая сила, компоненты которой, действующие в направлениях х, у и Z, выражаются следующим образом:

Х = -, F = -4, Z = -4. (2.8)

дх ду dz

Подставляя (2.8) в уравнение теории упругости для компонент смещения, написанное в векторной форме, получаем

(к + 2р) grad div ц - р rot rot и - grad р = 0. (2.9)

Преобразуя уравнение (2.9) с использованием формул векторного

анализа, получаем, что, как и в случае отсутствия объемных сил,

->-

вектор смещения и удовлетворяет бигармоническому уравнению

у2у2" = 0. (2.10)

При изучении механического взаимодействия горных пород и фильтрующейся в них жидкости в случае пластической деформации пород выражения (2.8) подставляются в уравнения равновесия, которые решаются с использованием тех же гипотез пластичности, что и при отсутствии массовых сил.