Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 [ 9 ] 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70

Если функция / (z) является аналитической в односвязной области, то интеграл (6.11) вдоль любого замкнутого контура, принадлежащего указанной области, равен нулю. Односвязной областью называется область, ограниченная одним замкнутым контуром. Пусть имеем односвязную область D, ограниченную контуром X (рис. 13). Функция / {£), аналитическая в области D, в точке а принимает значение / (а), а на контуре X - значение / {X). В теории функций комплексного переменного важное значение имеет формула Коши, согласно которой для аналитической функции / (z) имеем

(6.12)

Формула Коши позволяет определить значение аналитической функции в любой точке z, принадлежащей области, в которой функция аналитична, по значению этой функции на контуре области.

Интеграл, записанный в форме (6.12), в которой / (Х) является граничным значением функции, называют интегралом типа Коши. Подынтегральное выражение в нем стремится к бесконечности при Z -уХ, та. поэтому зтот интеграл считают существующим везде в области, где определена функция / (z), кроме самого контура, т. е. рассматривают его главное значение.

§ 7. УРАВНЕНИЯ И РЕШЕНИЯ ЗАДАЧ ТЕОРИИ УПРУГОСТИ

Имея уравнения движения элемента сплошной среды, легко получить уравнения теории упругости. Если тело является упругим, ему присущи следующие зависимости между компонентами тензоров напряжений и деформаций

Т«-Р {gz+ дх )

ди , dv , dw

, ( dv , ди\ (l+v)(l-2v) •

2(l + v) •

(7.1)

Входящие в (7.1) величины £ и v являются соответственно модулем Юнга и коэффициентом Пуассона. Символами и, v ш w обозначены компоненты смещения в направлениях х, у ж г.

При подстановке зависимостей (7.1) в уравнения движения получаем уравнения, описывающие упругие смещения. Записывая эти уравнения в векторной форме, имеем

(Я, 2р) grad div u - р rot rot и +

+ ЛГ-реа = 0, (7.2)

где М - вектор массовой силы; и и а - соответственно векторы смещения и ускорения.

В ряде случаев оказывается необходимым определять деформации, а не смещения. Тогда нужно, помимо уравнений движения или равновесия, использовать также систему уравнений неразрывности (совместности) деформаций. Эта система получается в результате последовательного дифференцирования зависимостей между компонентами деформации и смещения и соответствующих подстановок. Система уравнений совместности деформаций имеет следующий вид: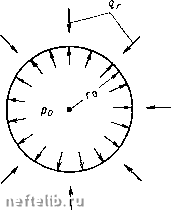

Рнс. 14. Деформация сферической полости:

?Р - горное давление

(7.3)

дУхг . . ду -Г

(дух.

дууг

дхду

дУуг\ о дех . дх ) dydz

дух2 \ 9 дЩ ду J " dx dz

В качестве примера рассмотрим упругую деформацию сплошной среды, простирающейся по всем направлениям до бесконечности, если в некоторой точке среды образована полость шаровой формы. Этот пример может относиться на практике к деформации полости, созданной, например, в горных породах в результате их размыва и выщелачивания. Пусть радиус полости равен го (рис. 14). Полость заполнена жидкостью или газом, оказывающими на ее внутреннюю поверхность давление ро. На большом расстоянии от полости (на

бесконечности) напряжение горных пород характеризуется равномерным сжатием. Будем считать, что смещения пород и напряжения являются центрально-симметричными. Массовые силы и ускорения отсутствуют. В этом случае уравнение (7.2) принимает следующий простой вид:

Имеем также две компоненты напряжения о, и Сте, определяемые зависимостями

(т, = (Я + 2р)-+2Я; ae = k + 2{k + ii);

0 = 420. (7.5)

Решая уравнение (7.4), получаем

0, = (3 + 2p)Ci-4p-; (Te = (3X + 2p)Ci-f 2р-,

где Ci и 6*2 - постоянные величины.

Выполним, в соответствии со сказанным выше, условия

о, = (Те = дг = const при г оо; (7.7)

(Уг = Ро при Г = Го.

В результате получаем следующие формулы:

Как видно из формул (7.8), напряжения о, и Oq убывают пропорционально кубу расстояния от центра полости. При ро = о имеем

(T, = gr(l-); cTe = gr(l-f4). (7.9)

При г = Го (Т, = О, а (Те = 3/2дг независимо от радиуса полости Го.

Оценим, например, прочность такой полости, используя в качестве критерия прочности предельную зависимость интенсивности касательных напряжений 5, от предельного среднего нормального напряжения а, в виде:

S*={i-+ {<У2-<ysf + -ОгПУ = а + Ьа, (7.10)

где а и b - постоянные коэффициенты. 34

(7.6)