Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 [ 43 ] 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63

На графе возможных путей развития лишь некоторые пути Aij являются кратчайшими цепями из Ni в Nj-, они принадлежат дереву графа. Предположим, что известна кратчайшая цепь из узла Ns в узел Nt. Тогда эта цепь должна состоять только из дуг дерева, в противном случае она не будет кратчайшей. Если теперь ввести дугу Ast с длиной, равной длине рассматриваемой цепи Ns - Ni, то эта дуга Ast будет также принадлежать дереву.

Задача нахождения кратчайших цепей между всеми парами узлов реализуется добавлением дуги дерева (если таких дуг в цепи не было).

Рассмотрим операцию получения дуги дерева относительно узла Nj-.

/fft = min(/(ft, lij h/ife) для 1фкф1 (П.21)

При этом сравниваются длина Uu Дуги Aih и длина цепи Ni~Nj - Nh. Затем длине дуги Aih присваивается значение Ijk + lij при условии

Если выполнить эту операцию последовательно для каждого узла Nj (/=1, 2, ,. ., п), то полученные в результате значения будут длинами кратчайших цепей между всеми парами узлов.

По мере последовательного выполнения операции (11.21) заполняется справочная таблица. Элемент (г, k) этой таблицы, стоящий на пересечении f-й строки и k-ro столбца, полагаем равным k. После выполнения операции (11.21) элемент указывает первый промежуточный узел в кратчайшей цепи между <V,-и Nil, если такой узел существует, в противном случае элемент (i, k) равен k.

Таким образом,

(i, k).

если если

(11.22)

Чтобы найти кратчайшую цепь из Ns в Nt, по справочной таблице сначала отыскивают элемент (s, t)=k, который означает, что узел Nk является первым промежуточным узлом в кратчайшей цепи из Ns в Nt. Затем находят элемент [к, t), который указывает первый промежуточный узел в кратчайшей цепи из Nh в Nt. Этот процесс продолжается до тех пор, пока ие будет найден элемент (t, t)=T, который означает, что найдены все узлы, входящие в кратчайшую цепь из Ns в Nt, а именно Ns, Nh, ..., Ni, Nt.

Если при выборе оптимальных трасс газопроводов и их разветвлений используется неориентированная сетка произвольной конфигурации, то для поиска многополюсных кратчайших ncncii на такой сотке допустимо использовать симметричные матрицы исходных данных, длин кратчайших путей и узлов прохождения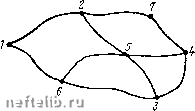

Рнс. 11.6, Сетка произвольной формы

для поиска кратчайших цепей

кратчайших путей. Это позволяет хранить лишь половину исходной и выходной информации, что существенно повышает эффективность применения рассматриваемого метода и его реализуемость на ЭВМ.

Следует отметить, что метод позволяет также сохранить произвольность распределения пометок графа.

Рассмотрим работу алгоритма нахождения кратчайших цепей между всеми парами узлов (рис. 11.6). Условимся, что дуги графа не ориентированы.

Длины дуг отрезков сетки заносятся в таблицу. Выполняем операции (11.21) (для /=1), заключающиеся в том, что определяются все элементы табл. 11.2, не лежащие в первой строке или первом столбце. Длины кратчайших цепей заносятся в табл. 11.3, а узлы прохождения пути -в табл. 11.4.

Z2e = min(/2e, /2i+W = min(oo. 16-Ь25) = 41;

«23 = min(/23, /2e + ies) = min (оо, 414-14) = 55;

/e7 = min(/e7. /e2 + 47)=min (оо, 4l4-8)=49.

Величины /25 и /56 своего значения не изменили.

Для / = 2 также выполняется операция 11.21, определяющая все элементы теперь уже табл. 11.3, не лежащие во второй строке и втором столбце, так как при этом используются результаты вычислений при /=1.

«i4 = min (/i4, /i7-f/74) =

/i4 = min (/i4, lib + ki)--

/l5 = min(/i5, ii2-f25) =

/i7 = min (/)l7, /12+ ki) =

/з7 = т1п (/з7, /35-1-/57) =

/57 = min (/57, /52 + /27) =

/e7=min (Св7, /в5+/б7)

/i3 = min(/i3, /15+ /53) = min (00, 28+13) =41;

= min (00, 24-f 11) = 35; = min (35. 28+10) = 38; = min(cc, 16 +12) =28; :min (00, 16 + 8) = 24; = min (00, 13+20) = 33; = min (00, 12+ 8)+ 20; = min (00, 9 +20) = 29. Величины /i6, /47. /56 своего значения не изменили. Для /=3: /23 = min (/23, I2, + /53) = min (55, 12 + 13) = 25; /24 = min(/2i, /25+/54)= min (00, 12 + 34) = 46; /4s = min(/46, /4з + /зв) = т1п (cx), 21 + I4) = 35.

Величины hi, Us, In, кь, Ui, hi своего значения не изменили.

Исходные данные о сети

I 2 3

Таблица П.2

16 О

оо оо

оо 12 21 О

оо оо 13 10 О

25 оо 14

оо 9 О

оо оо

2 3 4 5 6 7

Длины кратчайших цепей 1 2 3

Таблица 11.3

16 О

39 25 О

35 19 21 О

28 12 13 10 О

25 21 14 19 9 О

24 8 32 II 20 29 О

2 3 4 5 6 7

Узлы кратчайших цепей 1 2 3

Таблица 11.4

6 5 3

7 7 3 4

5 3 5 5 6

2 2 4 4 2 5 7

2 3 4

5 6 7

Для / = 4:

37 = niin (/з7, /з4 + /47) = т1п (33, 21+ 11) = 32;

/42 = min (/2, /474-/42) = min (35, li+8) = 19;

/46 = min (/46, /454-/56) = min (35, 10 + 9) = 19.

Всличипы /57, /б7 своего значения не изменили Для /=5:

/2e = min(/2e, /25 + /5e) = min (41, 12+ 9) = 21.

Величины /i3, /(4, /16, In, /23, Ы, /37, Im своего значения не изменили Результатом вычислений длин кратчайших цепей являются

данные табл. И.Зи справоч1юй табл. 11.4, с помощью которых

определяются узлы, входящие в кратчайшие цепи.

Пусть например, необходимо найти цепь из Ni в Л4. По

табл. 11.4 сначала находим элемент (1.4) =7, а затем (1.7) =2

л (1,2) = 1. Следовательно, кратчайшая цепь из Ni в N4 проходит через узлы М2 и Mj.

Таким образом, пользуясь табл. 11.4, .можно найти кратчайшую цепь между любыми двумя парами узлов. Для этого достаточно выполнить лишь некоторое число операций сравнения, равное числу дуг в искомом кратчайшем пути. Это дает существенные преимущества рассматриваемому методу, поскольку в предыдущих алгоритмах для отыскания кратчайшего пути из какой-либо точки необходимо строить дерево относительно этой точки.

Рис. 11.7. Варианты поиска

ЧТО при переборе начальных и конечных точек на сетке представляет трудоемкий процесс.

Проблема выбора оптимального разветвления трубопровода состоит не только в поиске оптимальных трасс участков между двумя пунктами, но и в определении места оптимального разветвления при отборе или притоке перекачиваемого продукта.

Для решения данной задачи будем исходить из следующих предпосылок.

Сеточная модель местности представляет собой возможные пути проложепия трассы и отвода или притока. При этом не делается различий для дуг проложепия трассы и отвода (притока)- каждая дуга может принадлежать как основной магистрали, так н отводу. Естествен1Ю, что дуги сетки не ориентированы.

Точка разветвления находится в одном из узлов сетки. В противно.м случае постановка задач не соответствует основной предпосылке - любые пересечения возможных путей проложепия трассы являются узлами сети.

Конфигурацию разветвления удобно рассматривать как три независимых участка, сходящихся в одной точке. При этом концевые точки каждого из участков являются исходными данными.

В зависимости от технологической схемы транспорта газа возможны сочетания вариантов диаметров трубопроводов разветвленной системы (рис. 11.7):

Di = D2 = D3; О.фО.фО;

(Dl = 0,)/\{0ф D,), (Dl = D,) Л (1 = D,),

{D.D,) Л (DaD,),

где Di, Dz, D3 -диаметр трубопровода соответственно первого, второго и третьего участков.

Алгоритмы поиска оптимального разветвления для перечисленных вариантов различны.

Рассмотрим наиболее простой случай, когда все диаметры трубопровода равны (0, = 02=Оз). Сетка представляет собой помеченный неориентированный граф С (А, N) (рис. 11.8). В общем случае каждая вершина множества вершин Ni = G{A, N) может рассматриваться как возможная точка разветвления Nst системы, а кратчайшие пути для трех участков могут находиться на ветвях дерева, построенного относительно этой точки разветвления в конечные точки участков Nt, (/=1, 2, 3).

Относительно вершин Ni по методу поиска кратчайшего пути на неориентированном графе осуществляется поиск кратчайшего пути в каждую из вершин Л- (У=1, 2, 3), т. е. строится дерево графа относительно вершины Ns. Построенное дерево позволяет отыскать кратчайшие цепи на участках Nsu Ntj (/=1, 2, 3) и определить их длину Lij или значение другого критерия оптимальности.

Суммарный кратчайший путь системы

(11.23)

Осуществляемый перебор вершин графа в заданной области разветвления позволяет отыскать вершину, удовлетворяющую условию

Lo= min Lt.

(11.24)

Выбранная таким образом точка разветвления будет оптимальной относительно заданного критерия. Если точка разветвления совпала с одним из узлов Nt) (/=1, 2, 3), т. е. отвод «вырождается», то рассматриваются два участка трубопровода.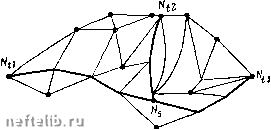

Рис. 11.8. Поиск оптимального разветвления

Рассмотрим алгоритм поиска оптимального разветвления системы для случая, если диаметры всех трех участков различны.

В этом случае для каждого участка строятся три графа Gi{AiN), GziAzN), GiAsN), соответствующие исходной сетке. Для этих графов существует взаимно однозначное соответствие между Ai, Аг и Лз.

Для графа GAiN) и отдельно для графа GiAiN) строится дерево ири значениях критерия оптимальности, соответствующих участку iVsi, iV(2, и отыскивается кратчайшая цепь на графе между этими точками, а также суммарное значение критерия оптимальности для найденного пути.

Разработанные алгоритмы поиска оптимальной трассы между двумя точками и алгоритм поиска оптимального разветвления системы .магистрального трубопровода позволяют перейти к решению более сложной проблемы - выбору оптимальных трасс системы магистральных трубопроводов со многими отводами.

Проблему выбора сложных трасс можно подразделить на две задачи: поиск оптимальных трасс трубопроводов с отводами ири заданной конфигурации системы и поиск оптимальных трасс сложных систем трубопроводов с выбором конфигурации системы.

Остановимся на реализации первой задачи, применив модификацию иерархического -метода оптимизации магистральных нефтепродуктопроводов. При выборе трасс сверхпротяженных трубопроводов длиной 2000-2500 км и более между двумя точками сетка разбивается на ряд фрагментов с граничными группами узлов. Эти группы рассматриваются как макрогруппы, если под макродугами подразумеваются участки оптимальной трассы между двумя смежными граничными группами. Расстояние между граничными группами рекомендуется принимать 400-700 км. Используя суперпозицию изложенного метода, можно рассчитывать трассы практически любой иротяженности.

Задана неориентированная сетка произвольной конфигурации с определенными начальными и конечными узлами трассы, а также конечными точками отводов (притоков) иа сетке и ори-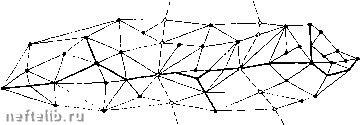

Рис. п.9. Конфигурация трассы с отводами:

- дуги графа;

разбиения графа; подграфов

- конфигурация системы;----условная граница

- конечные точки участков трассы; О - соединяющие вершины