Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 [ 12 ] 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177

p = pFf, (2.83)

dt с

dt дх,

df v"

и +-

= pFv + + pq,. Эх,-

Таким образом, система уравнений движения любой сплошной среды состоит из одного векторного и двух скалярных уравнений или пяти скалярных уравнений. В общем случае система уравнений (2.83) содержит 11 скалярных неизвестных : v, pij,p, и . Следовательно, она является незамкнутой. Это обстоятельство отражает тот факт, что в законах сохранения ие содержится никаких параметров, характеризующих свойства коикрстиых сплошных сред. Поэтому к полученным уравнениям необходимо добавить соотвстствующие соотиошеиия (связи), задающие физические свойства той или иной сплошной среды. Очевидно, что для разных сплошных сред (таких, например, как жидкость, упругое тело, пластическое тело и т.д.) эти связи будут иметь различный вид, и полученные, уже замкнутые системы уравнений для разных сплошных сред также будут имсть различный вид.

Установление необходимых для коикрстиых сред связей требуст предварительного изучения деформаций или скоростей деформаций сплошной среды.

Связи между иапряжеииями и деформациями или между напряжениями и скоростями деформаций называются реологическими уравнениями . Таким образом, различным сплошным средам соответствуют различные реологические уравнения.

В заключение заметим, что во всех рассуждениях настоящей главы предполагалось, что в классической механике сплошной среды принят постулат, согласно которому осиовиые законы сохранения считаются справедливыми ие только для всего рассматриваемого тела (в нашем случае -для материального объема), но и для каждой его части, сколь бы мала она ии бьша. Этот постулат носит название принципа локальности, а дифференциальные уравнения, являющиеся следствиями интегральных законов сохранения, называют локальными формулировками законов сохранения.

Заметим также, что если система координат, в которой рассматривается движение сплошной среды, подвижна, то все уравнения движения в этой системе координат сохраняют свой вид, только массовые силы будут включать в себя также и силы инерции, появляющиеся в относительном движении.

напряжение массовых сил F и тепловая мопщость представляют собой внепщие воздействия и

считаются заданными. реология (от греческого слова «течегше») - наука о деформацгш материалов.

системой уравнений, состоящей из (2.25), (2.42), (2.65) и имеющей вид р div У = О,

Глава III

СКОРОСТЬ ДЕФОРМАЦИИ СПЛОШНОЙ

СРЕДЫ

§1. Скорость деформации малой частицы.

Теорема Гельмгольца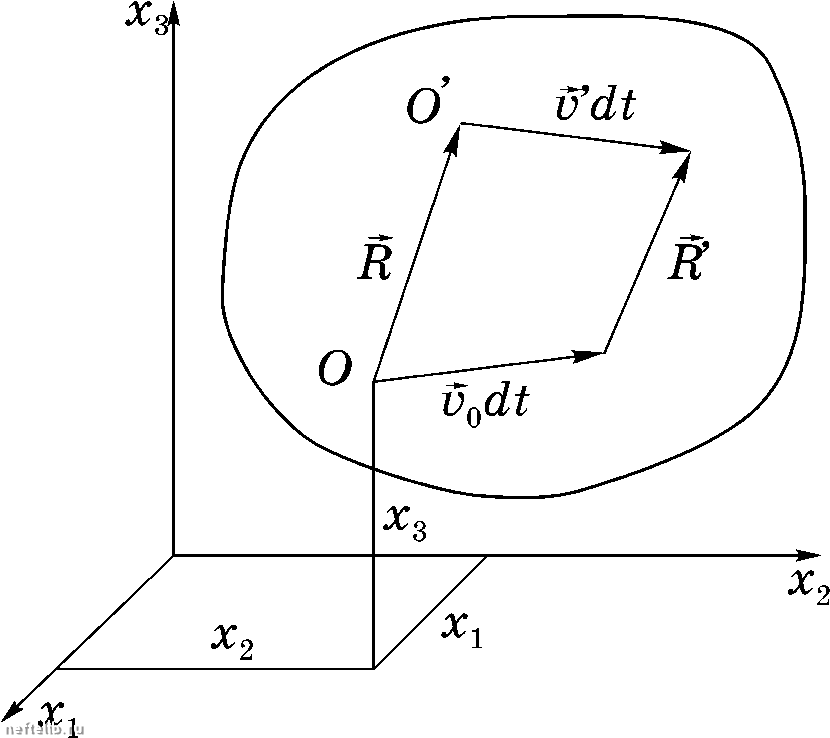

Рассмотрим малую частицу сплошной среды, изображенную на рис. 3.1, где точка О- центр частицы с пространственными координатами Ху, точка -тюбая точка внутри частицы, век-

тор R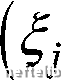

00 целиком лежит внут-

ри рассматриваемой частицы.

Распределение скоростей внутри частицы в фиксированный момент времени t\ определяется полем скоро-

Рис. 3.1

стеи, т.е. величинами скоростей точек О и О, соответственно, =u(xj,i)

и у = v[Xj +j,ti), или Voi = Vi(Xj,ti),

vl = vi[Xj + (j,ti). Движение в пределах

частицы предполагается непрерывным и дифференцируемым. Разлагая vl в ряд Тейлора, получаем

Эх..

+...

(3.1)

где все производные берутся в точке 0. Так как частица предполагается малой, т.е. предполагаются малыми в сравнении с характерным линей-

ным размером в рассматриваемой задаче, то, ограничиваясь в формулах (3.1) членами первого порядка малости, имеем

(3.2)

(3.3)

Из равенств (3.2) и (3.3) видно, что разность скоростей у - определяется матрицей

dXi dXj Эх-

(3.4)

элементы которой представляют собой коэффициенты при членах первого порядка малости в разложении vl в ряд Тейлора.

Матрица Ф всегда может быть представлена в виде суммы двух матриц, из которых одна симметрична, а другая аигисимметричиа. Действительно, введем обозначения

ik - -

= - 2

Эу, dVi

Эх-2 Эх

ydXk

d)-, = - 2

dV-, dVn

Эдгт Эх-

dXi Эх

(3.5)

Матрицу (3.4) представим в виде

Из формул (3.5) видно, что Siff. = £.

Подставив соотношение (3.6) в формулу (3.3), получаем

V = V,

DR + Пй.

Переписывая равенство (3.7) в координатном виде, имеем

V{ = V,, + 6-„i + £,242 + £п4з - Ohii + 0)23,

V2 = V,2 + 2lll + 222 + £233 + -

(3.7)

(3.8)

у, = у.

+ 322 + £333 - «2ll +

Из формул (3.5) следует, что величины представляют собой ком-поиеиты вектора а = ещ, который может быть символически записан