
 |
|
|
Главная Переработка нефти и газа ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА Из равенства (15.65) имеем А = Подставив эти выражения в соотиошеиие (15.66), получаем mk-ii)=-А--А = А А А А V, Исключая с помощью равенств (15.67) величины - и - А Рг лы (15.78), после элементарных преобразований получим 2k р. + 1 А или с учетом формулы (15.35) - (15.78) из форму- (15.79) (15.80) Соотиошеиие (15.80), связывающее значения скорости до и после прямого скачка, называется соотношепием или формулой Прандтля. Формулу Прандтля можно представить в виде = Л4 = 1 (15.81) Из соотиошеиия (15.81) следует, что формально возможны случаи: 1) > 1, < 1; 2.) Л = 4; 3) \ <\, >1. В соответствии с уравиеиием иеразрывиости (15.65) и формулой (15. имеем (15.82) Случай 3) соответствует условию < 1, то есть скачку разрежения, что, как бьшо показано, невозможно. Случай 2) означает, что р= - нет скачка. Случай 1) соответствует условию >1 , то есть ударной волне сжатия. Условия >1, 2 <1 означают, что перед скачком течение сверхзвуковое, а позади скачка - дозвуковое. 71.- 1 \k + \ Ар при М о= или Л J- будет ---> . \k-l р Изменение илотиости, как это следует из формулы (15.82), равно A/J Р2-Р1 .2 А А Для онределения изменения температуры воспользуемся соотношениями (15.43) и (15.83). Тогда, с учетом формулы Праидтля (15.81), получим %Т, т(Л) i fe;2 i fe;2 гт . + 1 2 При л, J-, то есть при У - . Однако это ие оз- иачает, что 72 . так как при v у 7] О. Поскольку при ирохождеиии газа через ударную волну эитрония возрастает, этот процесс сопро- Итак, скачки уилотиеиия (прямые ударные волны) могут возникать только в сверхзвуковом потоке. При ирохождеиии через прямую ударную волну сверхзвуковой поток переходит в дозвуковой. Обратное невозможно. Рассмотрим, как меняются параметры газа при его ирохождеиии через прямой скачок уилотиеиия. Из условия адиабатичиости процесса следует, что температура торможения до скачка Tq, равна температуре торможения после скачка 72 то есть %, = %2 = %. (15.83) Следовательно, Для онределения изменения давления воспользуемся адиабатой Гюгоиио (15.71) и формулой (15.82). Тогда + 1 Р2 I = = -1=4;=!--12/.-ifi-.(15.84) k-\ p. Заменяя в формуле (15.84) Л, с помощью соотношения (15.42), имеем .(Mi-l). (15.85) р, k+\ ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА вождается изменением давления торможения. Так как температура торможения при этом сохраняется, то в соответствии с уравнением состояния Менделеева-Клапейрона Ро2 Ро1 Р02 Р02 Р2 Pi Р01 Р2 Pi Poi На основании формул (15.44), (15.81), (15.82) последнее равенство мож- но представить в виде j2 (Л) 02 2 h-l 1 2 (15.86) Из формулы (15.86) видно, что при > I всегда а<1, то есть < Poi. Следовательно, механическая энергия необратимо перехо- дит в тепло, как это и должно быть при росте энтропии. Косой скачок уплотнения При изменепии направления пото- ка газа, например, нри обтекании клина (рис. 15.11), образуются так называемые косые скачки уплотнения. Фронт таких скачков расположен наклонно по отношению к направлению набегающего потока. В этом случае массовый рас- ход через единицу площади фронтовой поверхности OA, очевидно, равен (15.87) 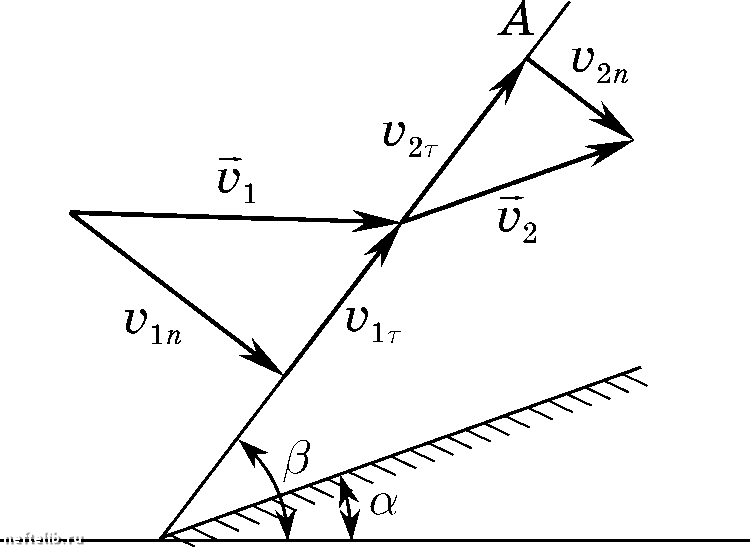 где и 1, V 2 - проекции скорости па нор- маль к плоскости скачка. Рис. 15.11 Закон изменения количества движения (2.54) запишем в виде m(v2 - = n(pi - Р2), (15.88) где п - единичный вектор нормали к OA. Закон сохранения энергии сохраняет свой вид (15.67). 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 [ 94 ] 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 |
||
 |
 |