Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 [ 19 ] 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177

Согласно требованию, накладываемому иа матрицу коэффициентов аф1,

комиоиеиты матрицы ие должны изменяться иа любом ортогональном иреобразоваиии. Поэтому должно выполняться равенство

ijkl - injmktlrnrntr ~ %kl (4-25)

комиоиеит в новой и старой системах координат. Рассмотрим, какое условие накладывает иа комиоиеиты матрицы аг равенство (4.25) иа иреобразоваиии (4.24). Для примера рассмотрим комиоиеиту оги- Имеем

%222 = / 2k 21 ijkl

После подстановки в иоследиее равенство комиоиеит матрицы иреобразоваиия (4.24) получим

(к222 = ~(к222

Поэтому условие (4.25) выполняется только при «1222 = О - Аналогично можно показать, что для выиолиеиия условия (4.25) иа иреобразоваиии (4.24) должны быть равны нулю все комиоиеиты матрицы Oikb которые содержат нечетное число индексов 2. Рассмотрев иреобразоваиия

1 О О") А О О

1 О О 1

О 1 О 0 0-1

получим новые ограничения иа комиоиеиты матрицы йуь которые сведутся к тому, что должны бьпгь равны нулю все комиоиеиты, содержащие нечетное число индексов 1 и 3. Следовательно, равенство (4.23) примет вид

Щ.1П Щ.122 1133

Й122 Й133

«2222 (2233

%233 (3333

%323

о о о

1313

1212/

£22 33 23

У12 J

Новые ограничения иа комиоиеиты матрицы можно получить, рассмотрев матрицы иреобразоваиия

Выполнение условия (4.25) иа этих иреобразоваииях приведет к тому, что должны выполняться равенства

«1111 = «2222 = «3333 «1122 = «1133 = «2233 «2323 = «1313 = «1212

и матричное равенство принимает вид

(4.26)

Наконец, рассмотрев преобразование, представляющее поворот иа угол 120" относительно оси г

- 1/2 л/з/2 О -л/з/2 -1/2 О О О 1

получим, что должно выполняться равенство

«1212 ~ ~ («1111 ~ «1122 )

Полагая а = Я + 2 , а = Я, получим, что ai2i2 = М (коэффициенты Я и называются константами Ламе).

Матрица коэффициентов в равенстве (4.26) в индексной форме записи представляется в виде

«ум = М/м + + iljk)- (4.27)

Подстановка тензора (4.27) в равенство (4.21) даст явный вид связи между тензорами е и Тц для изотроииой вязкой жидкости. Представление тензора вязких напряжений в матричной форме имеет вид

\ О О О 1 О О О 1

12 22 Т.

13 23 Т.

= Я div и

£l2

£22

£13 £23

(4.28)

V31 32 33 J

a в индексной форме задается равенством

Ту = Яdivl;y +2 %, £kk = div0. Подставив равенство (4.29) в формулу (4.21), получим окончательно Pij = -pSij + [ZSijSki + ju(SikSji + SiiSjk)\£ij = -pSij + ZSij£kk + 2jU£ij. (4.30)

(4.29)

ГЛАВА IV

Из формулы (4.29) видно, что вязкие свойства жидкости определяются двумя коэффициентами Я и . Если жидкость несжимаема, то div 0 = 0, и для несжимаемой жидкости имеется только один коэффициент . Как

следует из формулы (4.29), коэффициент ji влияет не только на касательные, но и на нормальные напряжения.

Просуммировав выражения (4.30) для нормальных напряжений р.

получим

, 2 Я + -

div0

-р + div0

(4.31)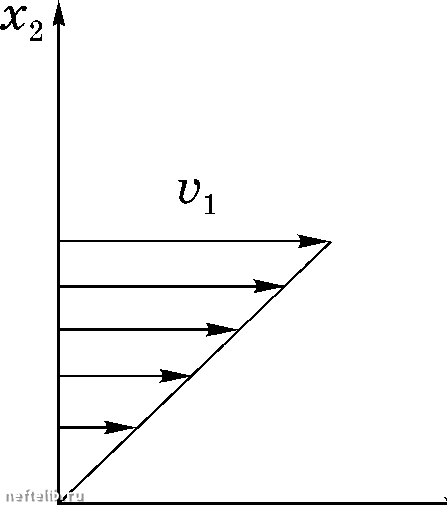

Величина = Я + - называется коэффициентом второй, или объемной, вязкости. В кинетической теории газов доказывается, что для одноатомных газов = О, но вообще С, .

Из формулы (4.31) следует, что для несжимае-

мои жидкости давление есть среднее арифметичес-

кое нормальных напряжении.

Рассмотрим в качестве примера установив-

Рис. 4.2

шееся течение, для которого поле скоростей имеет вид (рис. 4.2)

Vx = lfiX2, V2 =V2 = 0. (4.32)

Из равенств (4.32) следует, что

div V = -- = О,

1 dVx

2 Эхо

откуда, в соответствии с формулами (4.29), имеем

Рп = М

Рп - Рн - Рзз

Ри = Р23 = О •

Таким образом, в рассматриваемом течении происходит только скашивание углов, и это течение называется простым сдвигом. Величина

, как было ранее доказано, представляет собой скорость скаши-

2£

вания координатного угла и называется скоростью сдвига.

Из формул (4.32) следует, что линии тока - прямые х2 = const.

В соответствии с формулой (3.38) имеем

roti;

Эхз О

ез Э

Эхз О