Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 [ 170 ] 171 172 173 174 175 176 177

ПРИЛОЖЕНИЕ

Преобразование координат

Рассмотрим две прямолинейные прямоугольные системы координат 0xX2X2 и 0xX2X3 с координатными единичными векторами е, и ё2,ёз соответственно (рис. П.8). Назовем систему координат OXi старой, а 0xX2X3 - новой системой

координат.

Поскольку ноложение точки М в пространстве, или величина и наиравленне вектора а, нри нереходе

к новой системе координат не изменяется, то

М{х ,Х2,х) = М{х[, Х2, Хз \

к-кУ

(П.57)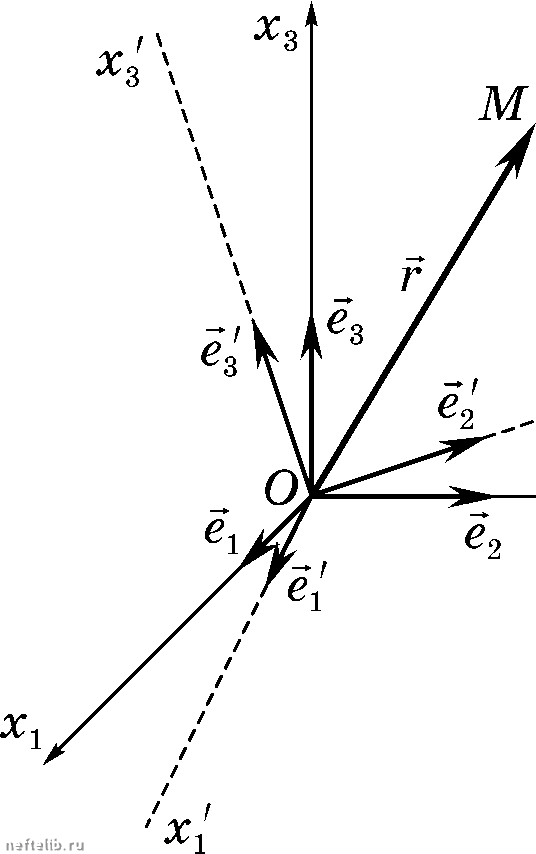

Рис. П8

или, что то же самое.

Умножив равенство (П.54) на е, а (П.55) на е, получим

ik •>

ki •>

cos(x;,xJ.

Для единичных векторов имеем очевидные формулы

ikiy к

Из формул (П.60) следует, что aj ф а

(П.58)

(П.59)

(П.60)

(П.61)

т- и ЧТО первый индекс в сим-

воле а относится к новым, а второй - к старым координатным осям В соответствии с равенствами (П.61)

ткт ткmi? ктт ~ kmimi

откуда

mkmi

iky kmim

<

1 при I = k, 0 при I Ф k.

Очевидно, что формулы (П.61) справедливы и для компонент векто-

ров.

V31 32 ззУ

Переход от новой системы координат к старой определяется матрицей

(П62)

«12 «22 «3

(П63)

V13 23 33 У

Матрица, в которой строки заменены столбцами, называется траиспо-иироваииой. Таким образом, матрицы (П.62) и (П.63) являются взаимно траиспоиироваииыми.

Тензоры

Для описания геометрических, или физических, объектов или процессов, происходящих в природе, используются геометрические или физические величины, которые обычно рассматриваются в той или иной произвольно выбранной системе координат. Так как реальные объекты и процессы существуют, очевидно, независимо от выбора системы координат, то и геометрические и физические величины, описывающие эти процессы, ие должны зависеть от выбранной системы координат. Таким образом, геометрическая, или физическая, величина, должна быть определена в каждой системе координат и должна задаваться в виде некоторой совокупности величии (компонент), но как математический объект должна быть независима от выбора системы координат. Это возможно в том случае, если задан закон преобразования компонент при переходе от одной системы координат к другой. В общем случае абстрактные математические объекты, иивариатгиые отиосительио преобразования координат, называются тензорами. Следовательно, геометрические (физические) величины являются тензорами. Простейшие тензоры - скаляр и вектор. Введем понятие тензора в наиболее простом случае, а именно, в прямоугольной декартовой системе координат.

Тензором ранга п называется совокупность 3" компоиет: а,, , , которые при переходе от одной системы координат к другой преобразуются по закону

а,, , = а.,а., ...а., а,, , . (П.64)

При этом подразумевается, что компоиетгы а,, , занумерованы индексами ![, гз,..., !, каждый из которых независимо друг от друга пробегает значения 1, 2, 3, а преобразование координат задается формулами (П.59).

Из формул (П.61) видно, что переход от старой системы координат к новой определяется девятью коэффициентами, из которых можно составить матрицу

Из приведеииого определения следует, что теизор нулевого ранга определяется одним членом, который сохраняет свое значение во всех системах координат. Следовательно, тензоры нулевого ранга представляют собой скаляры. Оии определяют физические или геометрические величины, характеризуемые только численным значением. Примерами скаляров являются температура, плотность, расстояние между двумя точками и т.д.

Тензоры первого ранга имеют три компоиеита, которые преобразуются по формулам

aj = aja. (П.65)

Так как формулы (П.65) совпадают с формулами (П.59) преобразования координат вектора, то тензоры первого ранга часто называют векторами. Однако вектор является лишь одним из примеров тензора первого ранга. Другим примером может служить плоскость в трехмерном простраистве. Ее положение задается тремя коэффициентами, которые, как легко видеть, преобразуются по закону (П.65). Следовательно, эти три коэффициеита образуют теизор первого ранга.

Теизор второго ранга определяется девятью компонентами, каждая из которых имеет два индекса, взятых в определеииом порядке. Для тензора второго ранга из формулы (П.64) имеем

а,, = а.,а., а,, . (П.66)

Суммирование в формуле (П.65) производится по иемым индексам il, гз. Поэтому, полагая = эту формулу можно переписать в виде

4 =«™«>а™. (П.67)

В дальнейшем рассматриваются только тензоры второго ранга.

В качестве примера тензора второго ранга рассмотрим теизор, построенный с помощью двух векторов. Пусть в системе координат OxiXx заданы векторы а = ёа и Ь = ё,Ь,. Рассмотрим совокупность всех произведений, содержащих иа первом месте компоиеиту вектора а, а иа втором -вектора Ь, то есть совокупность девяти величии а,Ь. В соответствии с формулами (П.59) имеем

то есть величины а,Ь действительно являются компоиеитами тензора второго ранга. Теизор второго ранга, образованный ио указанному правилу двумя векторами, называется диадой.

Тензору А с компоиеитами соответствует его матрица, в которой первым индексом принято обозначать номер строки матрицы, а вторым -номер столбца. Таким образом, матрица тензора имеет вид