Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 [ 168 ] 169 170 171 172 173 174 175 176 177

ПРИЛОЖЕНИЕ

откуда

/с J

Величины называются коэффициентами Ламе. Рассмотрим две бесконечно

близкие точки MviN, Проведем через точку М три координатные поверхности, которые вместе с тремя координатными поверхностями, проходящими через точку 7V, образуют бесконечпо малый криволинейный нар алл ел спине д (рис. П.5).

-►

Пусть MN = df. В соответствии с равенством (П.ЗЗ)

Эг , dg..

Эд,.

откуда, с учетом формул (П.З5) и (П.36),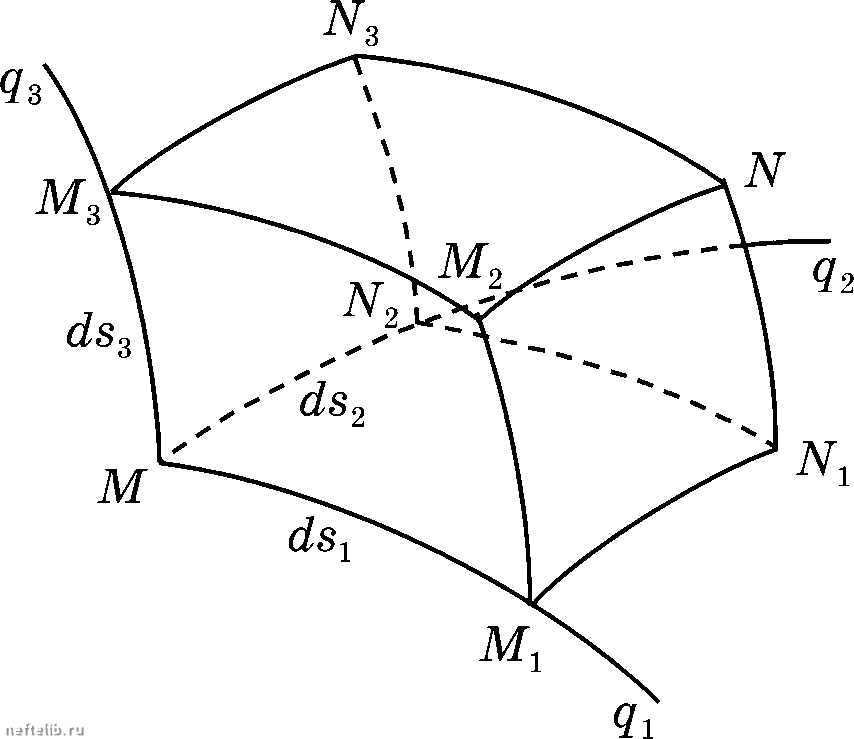

{drf = {dsf = {Hdqy,

Рис. П5

Вдоль линии ММ- 2 - const, 3 = const и, следовательно,

MMj = dSj = Hdq.

Аналогично

ds- = H-dq- (но i не суммировать!).

(П.37)

то есть формулы (П.37) позволяют определить длины ребер рассматриваемого параллеленипеда.

Параметрам Ламе можно дать и другое определение. Из рассмотрепия параллелепипеда на рис. П.5 и формулы (П.36) имеем

dg = eHdq,

откуда

dSj = Hdq

(П.38)

Площади граней MNNM, ММММ, MMNN, нерпендикулярных со-

ответственно осям gi,д2,дз5 равны

d(Tj - ds2ds3 - i2-f3 dq2dq2 у da2 = dsds = HH dqdq, d(j = dsds2 = HH2 dqdq2.

(П.39)

Объем нараллелепипеда равен

dV = dsds2ds = H 2H dqdq2dq

(П.40)

д(р 1 д(р

(по / не суммировать!)

(р = el

(П.41)

Для вычисления diva удобно воспользоваться формулой (П.27), приняв за объем Fобъем нараллеленниеда, иредставленного иарис. П.З.

На грани MNNM п = -ё1, и в соответствии с формулами (П. 19) и (П.38) поток через нее (с точностью до малых более высокого порядка) равен

- a,ds-,ds, = -a,H-,H,dQ-,dQ,,

а через грань MiMNNi -

Поэтому суммарный поток через грани, нернендикулярные оси , ра-

(П. 42)

Для граней, нернеидикулярных осям и , циклической иереста-

иовкой индексов имеем

Э(а2НзН1) diaHiH) /тт

" dqydq-,dq,, " dqydq-,dq,. (П.43)

Щ2 Эдз

Подставив в формулу (П.27) соотиошеиие (П.40) и сумму выражений (П.42), (П.43), после перехода к пределу получим

divd =

Н,Н-,Н-,

diaHH) diaHHJ) д{а-,НН-,

(П. 44)

Для вычисления rotd воспользуемся формулой (П.31).

Чтобы получить rot; d, то есть проекцию вектора rot d на координатную линию qi, нужно взять котгур, ограничивающий иоверхиость, нормальную к qi, то есть контур MNNM (рис. П.З), который обозначим через С;.

Очевидно, что с точностью до членов более высокого порядка малости

df = а-, ds-, = a-,H-,dQ-,,

Векторные операции в криволинейных координатах

По определению градиента (П.13) проекция вектора Vp иа коордн-иатиую ось q, равна , а так как ds, = H,dq, (по / ие суммировать), то

на кривой iVjiVj имеем

ddf = а-, ds-,

иа М,М

ddr = -

а-, ds-,

да, ds, dq-i

да-, ds-,

да,Н, dq-i

а-,Н-,

J \

daHi dq.

ddf = -a, ds, = a,H.

Суммируя эти выражения, получим

(П.45)

3 J

Подставив соотношение (П.45) и первое из равенств (П.39) в формулу (П.31), после перехода к пределу имеем

rot, а =

Н2Н, \

да,Н, да-Н-

и далее циклической перестановкой индексов получим

rot, а =

Н3Н1

да.Н, даН

rot, а =

"Ч1 J да-,Н-, да,Н,

(П. 46)

(П47) (П. 48)

12 )

Из формул (П.46)-(П.47) следует, что

rota =

И-,И-,

да-Н- да-Щ

daiHi даН-

dq, dq, ) Н,НЛ dq, dq ) ННЛ dq dq

da, Щ doi Hi

2 J

Ha H,a, H,a,

H,H-,H

Hjej Нзёз

Эд; Эд; HjOi Н,а, Ща,

Для вычисления оператора Лапласа в криволинейных координатах воспользуемся тем, что

Ад) = div{V д)). (П.50)