Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 [ 5 ] 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177

ГЛАВА I

а так как поверхность S произвольна, то

Рп (М) = -

(1.25)

Напряжение можно разложить на нормальную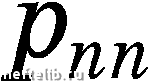

и тангенциа

ную р составляющие:

(1.26)

где т - единичный вектор п т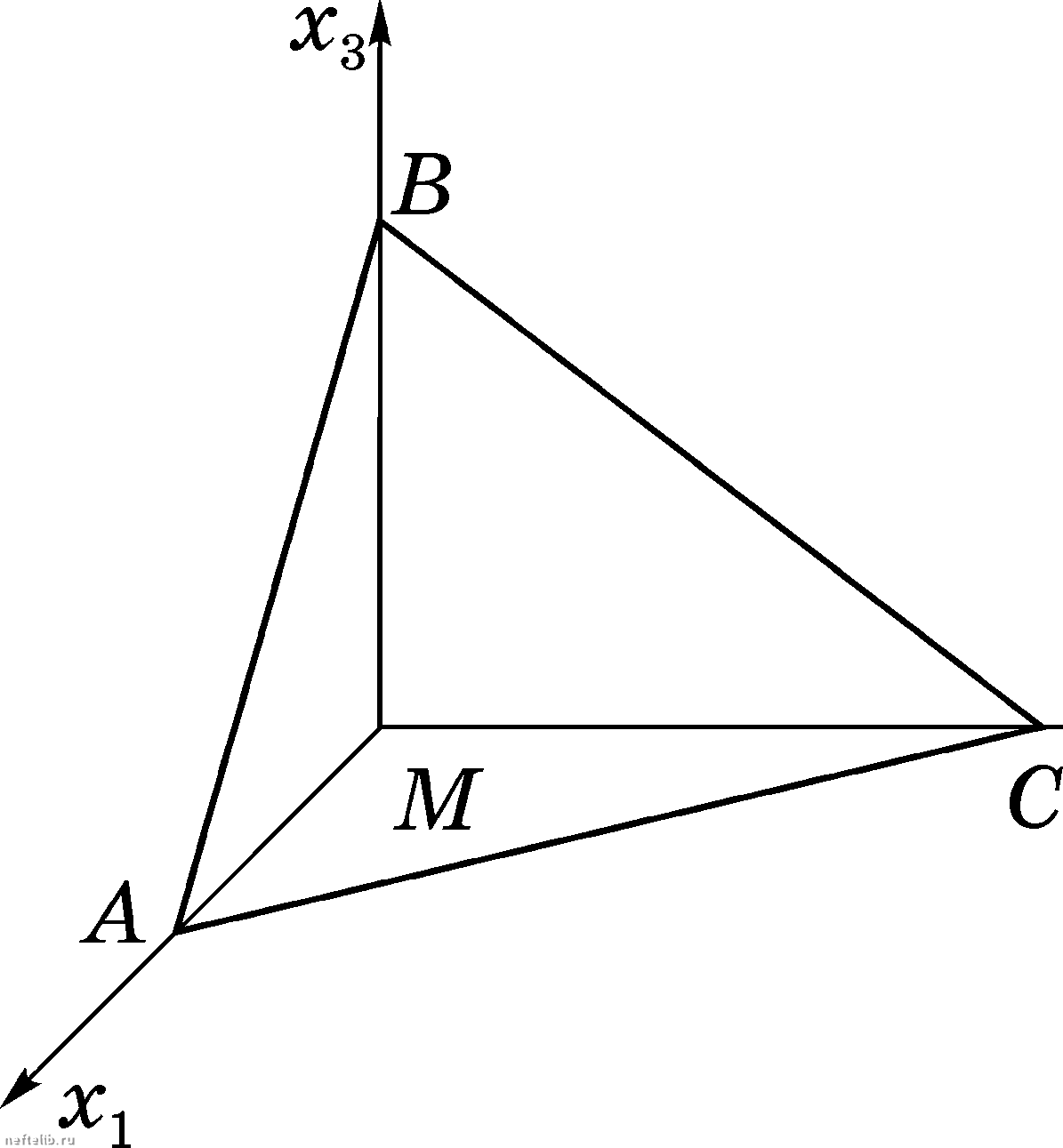

Возьмем какую-либо точку М сплош-

ной среды, проведем из этой точки координатные оси Xi, Х2, Хз и построим на них

бесконечно малый тетраэдр 5СМ (рис. 1.9) с ребрами dxx, dx2, с/Хз. Так как, по построению, грани тетраэдра ВСМ, АВМ, САМ

перпендикулярны соответствующим

там базиса, то п

еиП2

Ориентировка грани ЛВС произвольна и задается вектором нормали Я = eiai, где

Рис. 1.9

направляющие косинусы

нормали. Тогда напряжения на соответствующих гранях будут р 1 и р.

Обозначим площадь грани ABC через dS. Площади остальных граней можно вычислить как площади проекций грани ABC на соответствующие

координатные плоскости! dS\ - cxidS для грани ВСМ, 0,82 - cCn2dS

АВМ, dS - оСпфВ - для АСМ, или

ei)dS

(1.27)

На тетраэдр АВСМ будут действовать поверхностные силы P-idSi

и PndS, а также массовая сила dR

pFdV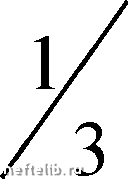

hdS, где

масса в объеме тетраэдра dV,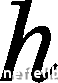

высота тетраэдра. В соответствии

со вторым законом Ньютона сумма сил, действующих на тетраэдр АВСМ, равна произведению его массы на ускорение, т.е. с учетом равенства (1.27)

phFdS

P-iCXidS

PndS

dv dt

dv dt

(1.28)

Сокращая все члены равенства (1.28) на dS и стягивая тетраэдр в точку (то есть полагая /г О), получим

P-ini

ИЛИ, с учетом формулы (1.25),

Pini

(1.29)

ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ

Векторы Pi можно представить в виде

Pi = jPji

(1.30)

где через Pji обозначена j-я компонента вектора Д.

Векторное равенство (1.30) эквивалентно следующим соотношениям в компонентах

Pnl ~ РппХ + PlXnl + РъХпЪу

Рп2 ~ РппХ + Pllnl + Рз2пЗу РпЗ - Punl + Р2Ъп2 + РъЪпЪ

(1.31)

Таким образом, напряженное состояние в точке определяется совокупностью трех векторов напряжения р, или их девятью компонентами Pij, определенными на трех взаимно перпендикулярных площадках.

Соотношение (1.29) является определением тензора (сам термин «тензор» происходит от французского слова tension, означающего напряжение).

Компоненты pj образуют тензор второго ранга, которому можно по-

ставить в соответствие матрицу

Рп Рп Ри Р21 Р22 Р23

Р31 РЪ2 РЪЪ

(1.32)

Первый индекс компоненты Pij тензора напряжений указывает на на-

правление координатной оси, параллельно которой направлен вектор нормали п, второй - направление координатной оси, на которую спроектирован вектор напряжения (рис. 1.10). Так, Р2\ представляет собой

проекцию вектора Р2, приложенного к пло-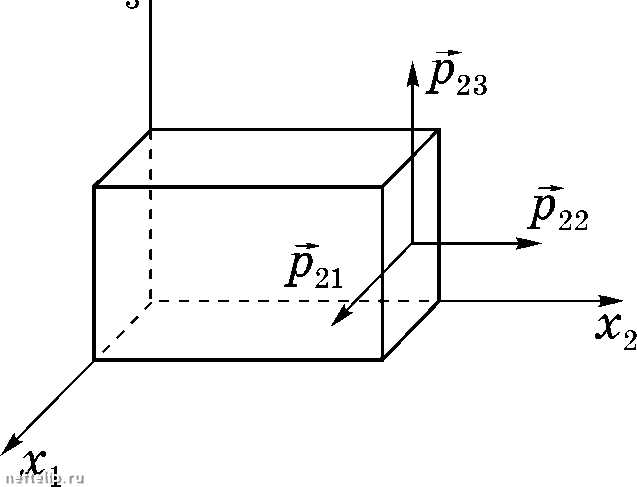

щадке, перпендикулярной оси Х2, на ось Xi.

Компоненты с одинаковыми индексами Рн называются нормальными напряжениями.

касательными

а компоненты Ри{1 Ф k) -

напряжениями, или напряжениями сдвига. Тензор напряжений Pij зависит от координат Xi и времени t и образует тензорное поле.

Заметим, что помимо изложенной классической теории напряженного

состояния, в которой считается, что моменты поверхностных и массовых сил в точке М равны нулю, существуют и более сложные теории, в которых рассматриваются сплошные среды с распределенными моментами поверхностных и массовых сил. Они рассматриваются в специальных разде-

lax механики сплошной среды, например, при изучении жидких и упругих сред с микроструктурой.

Глава II

ЗАКОНЫ СОХРАНЕНИЯ. ИНТЕГРАЛЬНЫЕ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ сплошной СРЕДЫ

§1. Интегральные характеристики сплошной среды и законы

сохранения

Основные уравнения для сплошной среды выводятся из законов сохранения, представляющих собой фундаментальные законы природы. В механике сплошных сред основными законами сохранения являются законы сохранения массы, изменения количества движения, изменения момента количества движения, энергии и баланса эигроиии. Для математической формулировки законов сохранения рассматривают или материальный (подвижный), или контрольный объем.

Под материальным (подвижным) объемом понимается объем, состоящий во все моменты времени из одних и тех же материальных точек.

Область иростраиства, через границы которой могут проходить вещество, энергия, количество движения и т.д., называется контрольным объемом, а поверхность, ограничивающая эту область - контрольной иоверх-иостью. Контрольная поверхность может перемещаться в пространстве, но обычно считается иеиодвижиой.

При рассмотрении материального объема считается, что ои представляет собой единое физическое тело, обладающее

массой М= \pdV, (2.1)

vit)

количеством движения J = jpvdV, (2.2)

Vit)

моментом количества движения М = (г х pv) dV, (2.3)

Vit)

энергией Е = j р

Vit)

u + - 2

dV, (2.4)