Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 [ 123 ] 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177

и системы координат, в которой записан обобщенный закон Дарси. Всегда можно выбрать хотя бы одну систему координат OxJCjj которой запись обобщенного закона Дарси имеет наиболее простой вид

К Эр*

Соотиошеиие (18.43) может быть записано и в матричном виде

(18.44)

(18.45)

Если принять соглашение о суммировании, согласно которому но повторяющемуся в записи индексу подразумевается суммирование, то соотиошеиие (18.43) можно записать более компактно

1 i,

щ = --k

(18.46)

где /ну принимают значения 1, 2, 3.

Система координат, в которой матрица коэффициентов проницаемости имеет диагональный вид и обобщенный закон Дарси записывается в виде (18.44), называется главной системой координат, а значения диаго-иальиых коэффициентов проницаемости к - главными значениями тензора проницаемости. В главной системе координат комиоиеиты матрицы обозначаются одним индексом, если система координат ие главная - двумя. Первый индекс соответствует номеру строки, второй - столбца.

В соотношении (18.46) выписано самое общее представление закона Дарси для анизотропных пористых сред. Уменьшая число отличных от нуля комиоиеит матрицы коэффициентов проницаемости, можно получить все возможные типы аиизотропии и изотропию. В самом деле, если положить, что все иедиагоиальиые элементы матрицы равны нулю, а все диаго-иальиые равны друг другу, то получим случай изотропных свойств. Все остальные варианты будут задавать разные типы аиизотропии. Прежде чем их классифицировать, определим свойство проницаемости в самом общем виде.

Проницаемостью пористой среды, по определению, (или иаправлеииой проницаемостью) называется величина к(п), которая определяется по формуле

к(п) = -

gradp

(18.47)

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ПОНЯТИЯ ФИЛЬТРАЦИИ

где п,

единичный вектор, задающий направление в пористой среде,

вдоль которого определяется паправлепная проницаемость, WiUi

(w • n)

скалярное нроизведение вектора скорости фильтрации и единичного вектора, grad р - модуль градиента фильтрационного давления. Как следует

из определения, в общем случае проницаемость может зависеть от направ-

ления.

Определение (18.47) имеет прозрачный фи-

зическии смысл - проницаемость, по определе-

пию, является скалярной величиной, которая вычисляется вдоль некоторого направления. Поэтому для того, чтобы ее вычислить, необходимо

найти отношение скалярных величин снециаль-ным образом определенных вдоль направления. В равенстве (18.47) в качестве направления.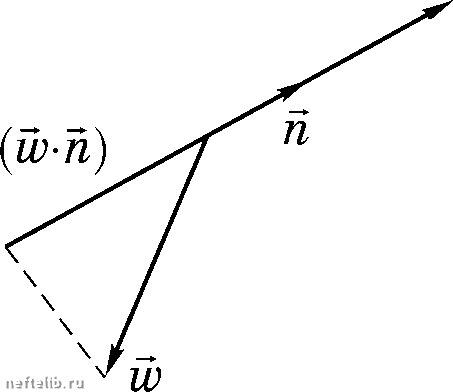

grsidp

Рис. 18.16

вдоль которого определяется свойство, рассматривается направление приложения градиента давления (gradр= gradр п), а скалярные величины онределяются проектированием па это наиравленне векторов скорости фильтрации и градиента фильтрационного давления. При проектировании па это паправлепие векторов iu и grad р получаем - ьищ и grad р , а их отношепие, умножеп-

пое на вязкость и взятое с обратным знаком, равно нроницаемости. Знак минус берется потому, что скалярное нроизведение ly.TZ. отрицательно

(угол между векторами w и щ тупой). Иллюстрация определепия иаправлеиной нроницаемости приведена на рис. 18.16.

Подставляя запись обобщенного на случай анизотропных сред закона Дарси (18.46) в равенство (18.47), получим

grad р

grad р

(18.48)

Соотношепие (18.48) дает общее правило вычисления проницаемости, которое справедливо как для изотропных, так и для анизотропных пористых сред. В самом деле, для изотропных пористых сред, по определепию (18.47) и правилу (18.48) вычисления нроницаемости в линейном законе

фильтрации, имеем

Следовательно, проницаемость для изотропных сред не зависит от направления (оиа для всех направлений одинакова и равна k).

Равенство (18.48) расшифровывает и смысл утверждения, согласно которому матрица коэффициентов нроницаемости kj онределяет и задает

фильтрационные свойства пористой среды. В самом деле, матрицы определяют тип свойств - изотропные или анизотропные, а числеииые значения ее элементов - величины, характеризующие их.

Как было показано, изотропные фильтрационные свойства задаются матрицей вида

(18.49)

следовательно, все возможные другие типы матриц задают анизотропные фильтрационные свойства. С помощью методов линейной алгебры можно показать, что все возможные вариатгы «анизотропных» матриц имеют вид

Первый тип матриц (18.50) задает фильтрационные свойства, например, слоистых (как правило, осадочных) пористых сред, у которых проницаемость в поверхностях напластований одинакова (плоскость с изотропными фильтрационными свойствами) и отличается от проницаемости в направлении, перпеидикуляриом к поверхностям напластований. Так как матрица имеет диагональный вид, то главные направления тензора коэф-фициетгов проницаемости у данного типа пористых сред известны априори - одно главное направление перпеидикулярио слоистости, два других -лежат в плоскости слоистости. В представлении матрицы коэффициентов проницаемости (18.50) направление, перпеидикуляриое напластованию, соответствует координатной оси OXj.

Второй тип аиизотропии задает пористую или трещиноватую среду, у которой априори, как и в первом случае, известны направления всех главных осей матрицы к-, но проницаемости по всем главным направлениям различны. Подобной анизотропией могут обладать трещиноватые коллекторы с тремя взаимно перпеидикуляриыми системами трещин, или уже упомянутые осадочные породы, образованные частицами вытянутой формы.

Первые два типа аиизотропии имеют специальные названия - первый тип называется траиверсальио-изотропиым, второй - ортотропиым.

В оставшихся двух типах аиизотропии априори неизвестно положение главных осей. В третьем типе неизвестно положение двух главных осей, в последнем случае неизвестно положение всех трех главных осей. По-видимому, реальные пористые и трещиноватые среды, как правило, к этим