Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 [ 3 ] 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177

откуда

dt dt dXj

dA diA dA ЭА ЭёА ЭА

dt dt dt dt dt dt

ЭА Эё.А ЭА V74i

e.Ui -- = --- = -= (v V)A

Эд: Эд: dx

= + (iV)A, (1.19)

dt dt

где (у V) - символический оператор, равный

(i;. V) = Vj

Первое слагаемое в формулах (1.12)-(1.15) и (1.18), (1.19) характеризует скорость изменения свойства А в фиксированной точке пространства и называется локальной производной. Второе слагаемое в этих формулах называется конвективной производной и характеризует изменение А за счет перемещения материальной точки в иростраистве. Величина конвективной производной определяется как движением материальной точки (v Ф О), так и неоднородностью распределения величины А в простраист-

ве(0). Эд:..

§4. Скалярные н векторные поля

Если в каждой точке области иростраиства D и каждому моменту времени t поставлено в соответствие значение скалярной (векторной) величины, то говорят, что в области D задано скалярное (векторное) поле.

где s°- единичный вектор касательной к траектории, v = efVi - вектор скорости.

С учетом выражений (1.16) и (1.17) формулы (1.14) и (1.15) могут быть представлены в виде

= + vVA. (1.18)

dt dt

Если А - вектор, т.е. А = еА, то в соответствии с равенством (1.14) dA.. ЭА.. ЭА..

ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ

Таким образом, под полем какой-либо величины понимается совокупность ее значений, заданных в каждой точке области D и в заданном интервале времени. Например, если заданы функции скалярных величин

p = p{Xi,t), T = T(xt,t), (1.20)

где р - плотность, Т - температура, то функции (1.20) определяют скалярные поля плотности и температуры. Если же дана векторная функция, например,

= Vk (Xi,t) или v = v(Xi,t), (1.21)

то функции (1.21) задают векторное поле скоростей.

Очевидно, что понятие поля физической величины применимо при описании движения только с помощью метода Эйлера.

Скалярное (векторное) поле называется непрерывным, если функция, его представляющая, непрерывна по и f. Если функция, представляющая поле, не зависит от времени t, то поле называется стационарным.

Если все поля, описывающие движение сплошной среды, стационарны, то такое движение называется установившимся или стационарным. Если же эти поля (или хотя бы одно из них) зависят от времени, то движение называется неустановившимся или нестационарным. При установившемся движении все локальные производные (частные производные по времени) равны нулю, т.е.

dt dt dt

Понятия установившегося или неустановившегося движения применимы только при описании движения методом Эйлера и являются относительными. Одно и то же движение может быть установившимся относительно одной системы координат и неустановившимся относительно другой. Например, при движении с постоянной скоростью твердого тела в жидкости движение жидкости будет установившимся в системе координат, связанной с телом, и неустановившимся в неподвижной системе координат.

Для любого векторного поля можно ввести понятие векторной линии. Векторной 1инией называется линия, касательная в ка-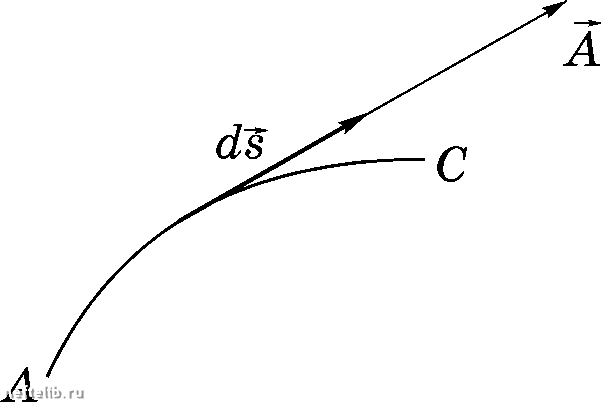

Рис. 1.2

ждои точке которой в данный момент времени совпадает с направлением вектора поля в этой точке. Из этого определения следует, что если задано векторное

поле A(Xit), то в точках векторной линии в данный момент времени выполняется условие А ds, где ds - бесконечно малый вектор касательной,

или ds = AdA, где dA - скалярный параметр (рис. 1.2).

ГЛАВА I

Векторные линии поля скоростей называются линиями тока. Так как

для них, по определению, ds

eidxi

eiVidA 5 то уравнения линий

тока имеют вид

doCj

ViiXjyt)

(1.22)

Заметим, что вдоль траектории движения материальной точки имеет

место равенство

Vi(Xj,t)

(1.23)

В соотношении (1.22) время является параметром, а в (1.23) - незави-

симой переменной.

Решение системы уравнений (1.22) имеет вид Xi = хДс/, А, t), где с.

константы интегрирования, и линии тока (векторные линии) в разные

моменты времени могут иметь разный вид.

При установившемся движении уравнения (1.22) и (1.23) принимают, соответственно, вид

dxi dA

dxi dt

и отличие сводится к разному обозначению параметра, по которому ведется дифференцирование. Следовательно, при установившемся движении

линии тока и траектории материальных точек совпадают.

Если решение системы уравнений (1.22) существует и единственно, то через каждую точку пространства проходит единственная линия тока. Од-

нако в некоторых точках поля скоростей условия существования и единственности могут нарушаться. В частности, условия единственности решения могут нарушаться в точках, в которых компоненты вектора скорости

обращаются в нуль или в бесконечность.

Рис. 1.3

Рис. 1.4