Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 [ 168 ] 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238

учитывалась форма контура области питания.

Допустим, что изображеппые па рис. 167 скважины Ai и А2 рав-подебитны. Положив в формуле (6, XX) Qi = Q2 = Q получим следующую формулу для давления в любой точке М пласта:

QV 2т:Ък

(1ПГ1Г2) + с

(38, XX)

Чтобы найтн уравненне изобары - уравнение геометрического места точек в пласте, в которых давления одинаковы, - следует в формуле (38, XX) положить р = const. Из формулы (38, XX) ясно, что давление будет одинаково в тех точках пласта, радиусы-векторы которых Г1 и г2 удовлетворяют следующему соотногаению:

Г1 • Г2 = const = С.

(39, XX)

Геометрическоз место точек, произведение расстояний до которых от двух заданных центров остается величиной постоянной, представляет собой кривую линию, называемую лемннскатной кривой или кас-синоидой или, наконец, овалом Кассннн (см., например, справочник по математике Бронгатейна и Семендяева [21]). Уравнение (39, XX) представляет собой уравненне лемнискатных кривых в биполярных координатах; различным значениям постоянной с будут соответствовать различные кривые одного н того же семейства.

Обозначая через хжу декартовы координаты точки и замечая, что

{X + 5f {X - 5f

(40, XX)

получим следующее уравнение семейства изобар в декартовых координатах:

(41, XX)

Как видно из последнего уравнения, лемнискатные кривые представляют собой кривые четвертого порядка.

На рис. 172 изображены лемнискатные кривые, причем кривым Si, S2 ... 8ъ соответствуют следующие значения параметра С:

для Sl,

С = 5 для 2,

С = I для Зз,

С = 22 для S4,

С = 36 для Зз-

Значению параметра С = 6 соответствует линия, называемая лемнискатой Бернулли. При 6 < С < 26 получаются бисквитообраз-пью кривью, окружающие обе скважииы и имеющие точки перегиба вблизи пересечения с осью у. При С > 25 получаются правильные всюду выпуклые овалы, окружающие обе скважииы и тем более приближающиеся по форме к окружности, чем больгае С. При С > 52 кривые распадаются на пары овалов, каждый из которых окружает соответствующую скв. А\ либо А. Хотя при С < 2 пи один из овалов точно не представляет собой окружности, но при малых значениях С эти овалы весьма мало отличаются от окружностей, концентричных скважинам. Если радиус скважип пе превыгаает О, 001, то с высокой степенью точности круговое сечение скважииы можно принять за овал, входящий в состав семейства изобар (с точностью по крайней мере до тысячной доли процента больгаая ось соответствующего овала равна малой).

Для овала, заменяющего круговое сечение скв. А\ (или 2), с упомянутой выгае степенью точности имеем:

ri=ic, Г2 = 2, C = 25Rc.

Расстояние, измеренное вдоль оси х между любыми двумя из изображенных на рис. 172 лемпискатпых кривых, всегда мепьгае соответствующего расстояния, измеренного вдоль оси у. Следовательно, в точках оси x скорости фильтрации больгае скоростей фильтрации в соответствующих (лежащих на тех же изобарах) точках оси у. Расстояние между соседними изобарами по оси х в направлениях от скважип к па-чалу координат больгае расстояний между теми же изобарами в противоположных направлениях.

Следовательно, в направлениях от скважин к началу координат скорости движения меньгае, чем в соответственных точках оси х (па тех же изобарах) в противоположных направлениях.

Вообще следует отметить, что на рис. 172 приведены лишь наиболее характерные и интересные по форме изобары. При построении изобар на рис. 172 не выдержано обычное требование (см. § 2 главы VIII) о равенстве прирагцений давлений при переходе от любой изобары к соседней. Поэтому, вообгце говоря, по густоте изобар на рис. 172 нельзя судить об изменении относительной величины скорости фильтрации.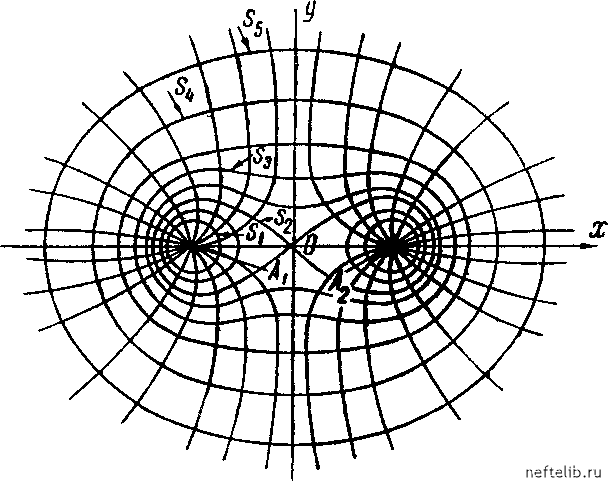

Рис. 172. Траектории и изобары двух равнодебитных взаимодействующих скважин.

Траектории (линии тока) можно построить либо как кривые, ортогональные к изобарам, либо воспользоваться графическим методом наложения (суперпозиции) полей, поясненным в § 2 главы XIX.

Рассмотрим, например, рис. 155, на которой пунктнрнымн и гатрихпунктнрнымн линиями изображены прямолинейные радиальные потоки одиночно работаюгцих скважин. Для изучаемого случая двух взаимодействуюгцих скважнн скорости фильтрации в любой точке потока, в частности и в изображенной на рис. 155 точке М, должны быть направлены по радиусам к скважинам. Направленне скорости V2 на рис. 155 следовало бы изменить на противоположное. Поэтому хорда траектории результируюгцего потока двух эксплуатационных скважин будет совпадать не с диагональю МТ четырехугольника NMST, а с диагональю NS.

В рассматриваемом случае траектории результируюгцего потока должны соединять те точки пересечения траекторий складываемых потоков, для которых сумма чисел (а не разность, как на рис. 155), стоягцнх около соответствуюгцих линий (траекторий складываемых потоков), остается величиной постоянной. Так, для точек N и S упомянутая сумма чисел одинакова н равна 9. Рекомендуем читателю самостоятельно выполнить но методу графического наложения полей построе-