Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 [ 59 ] 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238

Проинтегрируем последнее уравнение:

/ dr

(19, X)

откуда

(20, X)

Подставляя в формулу (20, X) z = he при г = Rc или интегрируя уравнение (18, X) в соответствуюгцих пределах, получим следуюгцую формулу дебита скважины:

wkjihl - hi)

(21, X)

Используя соотногаение (8, X), формулу (21, X) перепигаем так:

7гк8{2кк - s)

jl In

Rk Rc

А{2Нк8 - 5),

(22, X)

где для краткости соответствуюгцая группа постоянных множителей обозначена через А.

Подставляя значение дебита из формулы (21, X) в формулу (20, X), получим:

hi - hi

(23, X)

Уравнение (20, X) или (23, X) вполне определяет формулу воронки депрессии - свободной поверхности жидкости; тем самым уравнение (23, X) позволяет выяснить распределение напоров в пласте, ибо величина z равна напору в любой точке пласта с радиусом-вектором г.

Из формулы (23, X) вытекает, что z = const при г = const. Следовательно, поверхностями равных напоров служат боковые поверхности цилиндров, соосных скважине. Поскольку этот вывод является логическим следствием приближенного допугцения, следует помнить, что в действительности поверхности напора имеют более сложную форму.

Как видно из уравнения (23, X), депрессионная кривая является кривой логарифмического типа, но форма ее несколько отлична от той, которая была изучена в § 2 главы IX; именно, в формулу (23, X), в отличие от формулы (23, IX), входят вторые степени величии напоров.

Формулы (21, X) и (22, X) для дебита скважины называют формулами Дюпюи для случая притока к скважине жидкости со свободной поверхностью.

Из формулы (22, X) следует, что индикаторная линия имеет форму параболы; она изображена на рис. 64. Ось параболы направлена параллельно оси абсцисс. Вергаина параболы В отвечает значению s = h, т. е. максимально возможному понижению уровня в скважине - до ее забоя. Понятно, что нунктирпое продолжение BD параболической кривой не имеет никакого физического смысла - уровень жидкости в скважине нельзя опустить ниже ее забоя. Пупктирпое продолжение BD проведено для лучгаего понимания формы основного участка ОВ параболической кривой. Индикаторная кривая на рис. 64 соответствует также формуле дебита (9, X), выведенной в предыдугцем параграфе для случая притока жидкости к прямолинейной галлерее.

Для определения закона движения частицы жидкости вдоль траектории заметим [см. формулы (17, X) и (20, X)], что

2ттг

(24, X)

Подставим пайденпое выражение скорости фильтрации в формулу (10, VIII):

dr Q

27гг xlhl -

(25, X)

Разделим переменные г at и нроиптегрируем последнее уравнение:

2ттт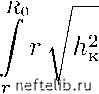

Qji

(26, X)

где Rq - расстояние движугцейся частицы жидкости от оси скважины в момент t = О, а г - расстояние той же частицы жидкости от скважины в момент t.

Интеграл, стоягций в правой части формулы (26, X), в конечном виде не вычисляется; его вычисление приходится выполнять либо с помогцью рядов, либо численными методами. Можно предложить такой приближенный прием вычисления интеграла: заметим, что значение подынтегрального радикала равно напору z в точке пласта с координатой г. Если разбить интервал интеграции на такие участки, внутри каждого из которых величина z меняется не очень сильно, то z можно вынести за знак интеграла. Так, например, беря небольпюй интервал интеграции в пределах от г = ri до г = Г2 и обозначая через z среднее значение напора в этом интервале изменений величины г, получим:

27rmz (Л

(27, X)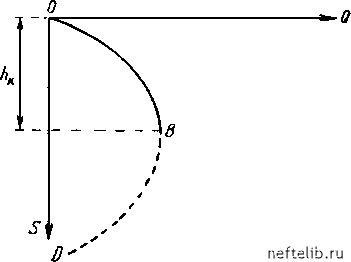

где At - промежуток времени, в течение которого частица жидкости переместится с расстояния Г2 до г\ от оси скважины.

Понятно, что упомянутый приближенный прием будет давать тем меньгаую погреганость, чем меньгае меняется величина z внутри интервала интеграции, т. е. чем дальгае этот интервал от скважины и чем меньгае величина самого интервала.

Подвергнем критическому анализу приближенное допугцение и некоторые основанные на нем формулы.

Считая траектории движения горизонтальными, Дюпюи учитывал кривизну депрессионных линий (кривизну свободной поверхности жидкости), которые также принадлежат к семейству траекторий.

Предположение о горизонтальности траекторий, строго говоря, несовместимо с основными особенностями движения жидкости со свободной поверхностью, в котором влияние силы тяжести должно сказываться на появлении вертикальных компонент скоростей фильтрации. Формулы дебита и рис. 64 указывают на то, что величина дебита стремится к своему максимальному конечному значению при s h, т. е. когда he 0.

Последнее означает, что могцность (высота) фильтрационного потока вблизи стенки скважины стремится к нулю, но тогда скорость

Рис. 64. Индикаторная диаграмма для скважины при притоке к ней жидкости со свободной поверхностью в условиях гравитационного режима.