
 |
|
|
Главная Переработка нефти и газа dS (х) Six) + = 0. (IX. 5. 42) da /i(a) vUia) (IX. 5. 43) Six) = -~\Ci-fia) 1(0) Уравнение (IX. 5.43) есть первый частный интеграл системы уравнений (IX. 5. 40). Оно дает зависимость х = х(а, Ci). Из второго уравнения системы (IX. 5. 40) получим * т5 (х) , . ... -W-- vS(x)f!(a) = (")• (1- откуда Исходя из начального распределения насыщенности, можно найти решение для дальнейшего распределения. Этот метод принципиально позволяет найти решение во всех случаях. Некоторые численные примеры приведены в работе Чэнь Чжун-сяна [9], который рассмотрел также случаи переменной проницаемости к = к (х) в этих задачах. Рассмотрим частные случаи. 1. у (х) = у = const, Q (t) = Q = const. Очевидно, что в этом случае уже не нужно вводить функцию (О. Из (IX. 5. 12) получается система уравнений dt mS (х) da ~ vS (х) /i (а) dx Q(t)t {a) + vS(x)t[{a) =--vS (x)t, (a)-• (IX. 5. 39) В этом случае можно решить систему уравнений (IX. 5. 12) иным способом. Перепишем (IX. 5. 39) в виде - = - + . (IX.5.40) da vfi(a) Из первого уравнения системы (IX. 5.40) имеем = "" И (IX. 5. 41) da vS (X) /i (О) Уравнение (IX. 5.41) есть обыкновенное линейное уравнение первого порядка. Его решение имеет вид  Рис. IX. 22. 2. у (х) = у = const, S (х) S = const. При движении в трубке тока постоянного сечения S (х) = S = = const система уравнений (IX. 5.12) примет вид: " Q(t)t(o) + iSf[(a) Ее общее решение ст, X- / (С) jQ{t)dt + vSf, {a)t (IX. 5. 47) = 0. (IX. 5. 48) Рассмотрим практический пример. Пусть пласт имеет наклон а к горизонту (рис. IX. 22). Вдоль горизонтальных линий тока у = 0; вдоль наклонных линий тока в нанравлении а согласно (IX. 5.10) у = ± i - sin а. Через скважину, расположенную в центре пласта, заполненного одной жидкостью, нагнетается другая жидкость. Пусть Q = const и вначале пласт полностью заполнен одной жидкостью. Будем считать в нервом приближении, что трубки тока остаются плоско-радиальными. Дифференциальное уравнение (IX. 5. 20) движения фронта имеет вид: mS{x) = Qt (а) + у5(х)/; (а). (IX. 5. 49) Общее решение системы уравнений (IX. 5.40) будет W Г/ (X) + 4 / - / Ф1 ст1 = О, (IX. 5. 46) где W - произвольная функция. На фронте вдоль наклонных прямых i = ± sin а должно удовлетворяться условие (IX. 5. 21): mS (х) -] = Qf (Оф) ± vS (Хф) /; (Оф) = = Qf (Оф) ± vS (Хф) и (Оф) Таким образом, имеем Qf (Оф) ± vS (Хф) /; (Оф) = /«Ф)(Ф)/1«Ф) . (IX. 5.50) Предположим, что на фронте Qi, v, S (х) - известные функции. Задаваясь разными значениями х, по формуле (IX. 5.6) Qi = Qf{a)±vS{x)U{a) при Q = const можно построить зависимость Qi от а (рис. IX. 23). На рис. IX. 23 из начала координат проводим касательную к кривой Ql (о). Величина а для точки касания согласно (IX. 5. 23) есть фронтовая насыщенность, которая, таким образом, при а О зависит от X. Расчеты показывают, что при малых углах а и достаточных темпах нагнетания изменение фронтовой насыщенности от значения, даваемого теорией Баклея - Леверетта, т. е. при v (х) = О, незначительно и его в первом приближении можно не учитывать. Если же темп нагнетания мал, то это изменение становится существенным и фронтовая насыщенность при учете гравитации, т. е. когда V (х) Ф О, отличается от значения, получаемого без учета гравитации по теории Баклея - Леверетта. Некоторые расчеты движения скачков насыщенности приведены в [17], а также в работе Чэнь Чжун-сяна [9]. Везде выше обе жидкости предполагались несжимаемыми. Точный учет сжимаемости, когда одна из фаз является газом, наталкивается на серьезные математические трудности и поэтому приходится идти на различные упрощающие допущения, например использование метода последовательной смены стационарных состояний и его разновидностей, соображений материального баланса и т. п. 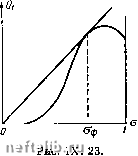 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 [ 113 ] 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 |
||
 |
 |