Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 [ 67 ] 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131

(VII. 8. 4)

разность объемных весов воды и нефти.

Используем теперь условие, что вода неподвижна, и, следовательно, давление в ней распределено гидростатически по закону Паскаля. Обозначим высоту конуса у, тогда у = h - г.

Рассмотрим две точки (рис. VII. 14, а): вершину конуса (точка А) с давлением р и точку пересечения оси скважины с первоначально невозмущенной поверхностью раздела (точка А). Давление в точке А согласно закону Паскаля равно

Ра = Р+УвУ- (VII. 8. 6)

Пусть на некотором расстоянии от скважины Ло мощность нефтяного пласта равна h и известно давление Ро на границе раздела. Тогда, так как вода неподвижна

P = Pj,,-yy = P-y„(h-z). iWn.S.I)

Выражая давление через потепциал Ф нефтяной части пласта согласно формуле (VII. 8.3), получаем

Po = -j-o+ynh, (VII. 8. 8)

где Фо-потепциал точки с давлением р.

Тогда уравнение (VII. 8. 7) можно представить так, учитывая (VII. 8.3):

ф + ун2=-- Фо-ЬТнЛ-Yb (h-z) или согласно формуле (VII. 8-5) и рис VII. 14

JLф = JLф-У(h~z) = Фo-yy. (vii.8.9)

причем знак плюс относится к случаю, когда ось z направлена вертикально вверх, а минус, когда она направлена вертикально вниз. Для наших условий, когда ось z направлена вниз:

Ф = -у(р~Увг), (VII. 8. 2)

где Л-проницаемость; [г -вязкость нефти; ун -удельный вес нефти. Из формулы (VII. 8-2) находим

Р = -рФ + Ун2, (VII.8.3)

после чего условие устойчивости конуса (VII. 8.1) принимает вид:

fi дф ,

дф кАу ~дГ где

Ау = Уъ-Уи. (VII. 8. 5)

Из формулы (VII. 8-9) получаем

(VII. 8. 10)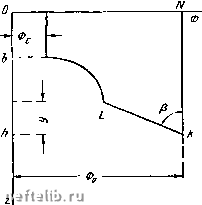

т. е. вдоль границы раздела текуп1ей иефти и неподвижной воды потенциал изменяется линейно в зависп.мости от высоты.

На рпс. VII. 15 приведены кривые распределения потенциала вдоль оси скважины и вдоль цилиндрической поверхности Ro- Величина потенциала отложена вправо, как показано на рис. VII. 15. Вдоль поверхности До потенциал будем считать постоянным: Ф = Фо (прямая KN).

Уравнение (VII. 8. 10) изображается прямой линией KL, наклоненной к вертикали под углом р, с угловым коэффициентом, равным tgP = kAy/ii. Где-то на этой прямой лежит потенциал вершины конуса. Если бы была известна высота подъема конуса, то сразу можно было бы найти этот потенциал.

Теперь посмотрим, какой вид будет иметь распределение потенциала в нефтяной части пласта.

Наименьшее давление, а следовательно, и наименьший потенциал будут на стенках скважины, причем вдоль стенок скважины потенциал считается распределенным равномерно, так как на стенке скважины давление можно считать гидростатическим. Обозначим потенциал на стенке скважины Фс. Ниже донышка скважины потенциал будет возрастать.

Нетрудно показать, что потенциал вдоль оси будет возрастать так, как показано на рис. VII. 15, т. е. выпуклостью вправо.

Действительно, вертикальная составляюп1ая скорости фильтрации определяется формулой Wz =- -д Ф.дг.

Вершина конуса по условию неподвижна. Следовательно, скорость нефти на этой вершине обращается в нуль, откуда вытекает, что касательная в этой точке должна быть вертикальной.

К оси скважины подтекают струйки. Поэтому скорость вдоль оси скважины монотонно возрастает от нуля до какого-то максимума на донышке. Таким образом, I д Ф1дг I вдоль оси z скважины монотонно возрастает и кривая распределения потенциала Ф = Ф (О, z) должна быть обращена выпуклостью вправо, как показано на рис. VII. 18.

Очевидно, высота конуса определяется положением точки пересечения прямой KL и кривой Ф = Ф (О, z).

Точный вид распределевия потенциала при наличии конуса обводнения неизвестен. Поэтому нужно исходить из каких-то других предпосылок, которые позволят оценить хотя бы приближенно величину подъема конуса и наиболее интересную для практики величину - предельного безводного дебита.

Заметим попутно, что эта задача имеет много общего с некоторыми задачами безнапорной фильтрапии, о частности с задачей о гравитационном притоке жидкостей к несовершенной скважине (рис. VII. 16).

Предположим, что водоносный пласт с открытой поверхностью эксплуатируется при помощи скважин, которые перфорированы в нижней части.

Рис. VII. 15. Распределение потенциала вдоль стенки скважины, ее продолжении и поверхности водяного конуса.

Прямая АВ изображает статический уровень грунтовых вод. Если скважина совершенная и вскрыла пласт полностью, - мы имеем задачу о безнапорном притоке к колодцу (см. гл. VI), когда дебит выражается формулой Дюпюи. Если же скважина перфорирована в нижней части, то поверхность депрессии - поверхность грунтового потока - будет иметь вид кривой АССВ, т. е. над фильтром будет, как говорят гидротех-пики, некоторая величина нависа-ния у.

При слишком большом дебите поверхность депрессии понизится до верхнего отверстия и туда прорвется почвенный воздух.

Эта задача и задача о конусе подошвенной воды в нефтяной скважппе совершенно эквивалентны. Роль подошвенной воды .здесь играет почвепный воздух.

Рассмотрим приток жидкости с образованием неподвижного устойчивого конуса подошвенной воды и проведем две цилиндрические поверхности, соосные со скважиной: первую некоторым радиусом го (в частности, это может быть радиус скважины); вторую радиусом Ло (рис. VII. 17, а). Направим ось z вниз п иа произвольном расстоянии г (го < г<; Ло) опишем цилиндрическую поверхность вокруг скважины; найдем расход нефти через эту цилиндрическую поверхность.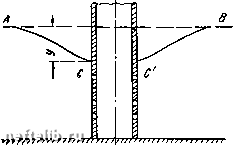

Рнс. VII. 16. Схема газового конуса.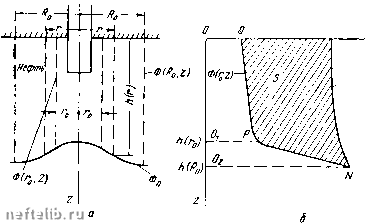

Рис. VII. 17.

Обозначим высоту этой цилиндрической поверхности h. Она будет переменной величиной: h = /» (г). Напомним вывод одного из интегральных соотношений для расхода (§ 6, гл. VI) применительно к нашей задаче.

Дебит жидкости (нефти), протекающей через нашу цилиндрическую поверхность, можно определить следующим образом. Выделим бесконечно малый элемент поверхности - цилиндр - высотой dz и радиусом г и найдем элементарный расход через боковую поверхность этого цилиндра.