Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 [ 53 ] 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131

д=1р(я:-я:). (VI. 2.4)

Далее из формулы (VI. 2. 2) находим

(VI. 2. 5)

Если вместо q подставить значение расхода из формулы (VI. 2. 4), то получится

Л=/я:-1=.. (VI.2.6)

Таким образом, согласно гидравлической теории безнапорного движения поверхность депрессии является параболой, показанной пунктиром на рис. VI. 1 (кривая АС).

Формулы (VI. 2. 5) и (VI. 2. 6), т. е. уравнения для поверхности депрессии, которые даются гидравлической теорией, вообще говоря, несправедлИвы.

Это ясно из следующих соображений. Из (VI. 2. 6) при Яг = О у выхода в нижний бьеф {х = I) получаем А = О и, следовательно, бесконечную скорость фильтрации qlh, что физически невозможно. Таким образом, в действительности должно быть hx=i Нг, Т- е. должен существовать промежуток высачивания.

Формула же для дебита (VI. 2. 4), хотя и выведена на основании приближенных допущений, тем не менее является точной, как будет показано ниже.

§ 3. Гидравлическая теория безнапорного притока к совершенной скважине

Рассмотрим теперь схему установившегося безнапорного притока к совершенной скваншне или колодцу при горизонтальном водоупоре (см. рис. VI. 2).

Пусть на расстоянии i?„ уровень грунтовых вод равен Я„. В самой скважине устанавливается уровень Не.

Проведем цилиндрическую поверхность радиусом г, высотой h. Скорость фильтрации будет направлена к оси скважины в сторону убывания г, и согласно формуле (VI. 1. 4) мы должны были бы записать ее следующим образом:

В каком-либо другом сечении, например в нижнем бьефе на расстоянии /, Он определяется уровнем Яг в нижнем бьефе. Из формулы (VI. 2. 2) получаем

ql = -{H\-Hl) (VI. 2.3)

S 4. Строгое доказательство формул Дюпюи для безнапорного движения 163

Найдем расход жидкости через боковую поверхность цилиндра. Расход будем считать положительным, когда скважина являетсй скважиной-стоком:

д==\11?г\2ягк = с ~2я rh. {VI.3.1)

Знак минус здесь не нужен, так как мы условились считать скважину стоком и А = А(г) - возрастающей функцией расстояния.

Движение, как и раньше, считаем установившимся. В каждом поперечном сечении Q, А (г) от времени не зависят.

В уравнении (VI. 3. 1) разделим неременные:

0 = 2Kchdh. г

Интегрируя, получаем

(?1пг= ясА-bconst. (VI. 3.2)

Постоянная (const) находится из условий на контуре питания Н: In i?„ = я сЯк -- const,

откуда

Qhi = nc{Hl - h\ (VI. 3.3)

Если это уравнение разрешить относительно А, то получится уравнение кривой депрессии (пунктирная кривая АССА). Для дебита жидкости получаем

лс(Я-Я

Q= д • (VI. 3.4)

In --~

Формулы (VI. 2. 4) и (VI. 3. 4) называются формулами Дюпюи. В дальнейшем мы увидим (§ 7, гл. VI), что теория безнапорного движения грунтовых вод имеет аналогию с совершенно другой задачей подземной гидравлики - задачей фильтрации газов в пористой среде. Эта аналогия была установлена Л. С. Лейбензоном.

§ 4. Строгое доказательство формул Дюпюи для безнапорного движения через перемычку и притока к скважине

Как уже упоминалось, формулы (VI. 2. 4) и (VI. 3. 4) для дебитов очень близко совпадают с результатами опытов [Лт. I. 111.

Уравнения же кривых депрессий (VI. 3. 3) и (VI. 2. 5) вдали от скважины и от выхода в нижний бьеф удовлетвррительно совпадают с опытами и точной теорией. Расхождение наблюдается в непосредственной близости к скважине или к выходу в нижний бьеф.

Формулы для дебитов (VI. 2. 4) и (VI. 3. 4) тем не менее являются совершенно строгими и точными. Это было установлено автором в 1951 г. [3].

Рассмотрим грунтовой поток при горизонтальном водоупоре. Напишем точную формулу для расхода жидкости через сечение глубиной h, шириной в единицу. г Возьмем на высоте z полос-

ку dz (рис. VI. 4). Элементарный расход через элемент dz равняется

dqudz. (VI. 4.1)

Полный расход через все сечение получится интегрированием элементарных расходов. Пределы интегрирования будут от нуля до h: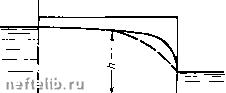

Рис. VI. 4. Кривые депрессии при действительном течении (сплошная) и течении по гидравлической теории безнапорной фильтрации (пунктир).

g = f udz.

(VI. 4.2)

Далее по закону Дарси горизонтальная составляюш;ая скорости равна

и = - с

дН дх

(VI. 4.3)

где Н = z-\-

Следовательно,

q = -

дН , с dz = - с

д I р

дх \ у

dz. (VI. 4. 4)

Коэффициент фильтрации считается постоянным и его можно вынести за знак интеграла. При этом не делается никаких гипотез о характере распределения давления по вертикали; оно может быть гидростатическим и не гидростатическим.

Далее воспользуемся известной формулой дифференцирования определенного интеграла по параметру [Лт. III. 7]:

Ф2 (а)

Ф2 W

f(z, a)dz =

df(z. а) да

dz + fif, -)~fifu а)