Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 [ 59 ] 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131

где т - пористость. По этим скоростям и будет производиться в дальнейшем расчет движения отмеченных частиц, границы раздела двух жидкостей и т. д. При этом будут получаться принципиально правильные результаты для интегральных характеристик - расходов и средних скоростей. Истинные же скорости частиц могут отличаться от этих средних.

В рассматриваемых ниже задачах этой главы жидкости предполагаются несмешивающимися, взаимно нерастворимыми и химически не реагирующими одна с другой и с пористой средой. Вытеснение одной жидкости предполагается происходящим полностью - так называемое «поршневое» вытеснение. Это также является идеализацией, так как в действительности полного вытеснения не происходит. Задачи, в которых учитывается неполнота вытеснения, рассмотрены в главе IX.

§ 2. Уравнения движения отмеченных частиц в потоке однородной жидкости

Рассмотрим уравнения движения отмеченных частиц в потоке однородной жидкости.

Пусть дана однородная жидкость, потенциал движения которой Ф {х, у, Z, t) известен.

Истинная скорость движения частицы , скорость фильтрации

W = т, где ds - элемент траектории.

Тогда уравнения движения в координатной форме могут быть записаны в виде

dx дФ , ,

"чг = -= /i У. 2- t),

1 = - = /2( 2/- 2.0. (VII. 2.1)

dz дф , ,

= "~ ~аГ 3 У. Z, t).

Функции /i, /2, /3 известны, поскольку потенциал Ф{х, у, z, t) считается заданным.

Интегрируя систему (VII. 2. 1), получаем закон движения или траекторию жидкой частицы в виде x = x{t), y = y{t), z=z{t).

Интегрирование производится особенно просто, если скорость есть известная функция одной величины s:

ds , ,

Можно поставить более широкую задачу о движении жидкой линии или жидкой поверхности.

т т т

на оси X, у, Z.

Требуя, чтобы эти частицы остались иа жидкой поверхности, имеем

р(х+-Ы, y + -bt, z + bt; «-Ь6«) = 0.

Развертывая это соотношение в ряд Тейлора и удерживая члены

с первой степенью 61, получаем

р / ..4 1 X t dF , V а i dF . w , dF . , . dF

r (X, y, z, n -f- - 0 i -t:----ot -- - 0 £ -hot -- = 0,

m dx m dy m dz dt

откуда, так как F(x, у, z, t) = 0 no условию, устремляя bt к нулю,.

получаем

dF , dF , dF , dF „ /тгтт о o\

" + + " + -аГ = 0 (Vn.2.3>

или, заменяя скорости через производные потенциала,

отgrad Ф grad/" = 0. (УП.2.4>

Линейное дифференциальное уравнение в частных производных первого порядка (УП.2.3) представляет собой соотношение Кельвина,. удовлетворяюш,ееся на всякой поверхности F {х, у, z, t) = О, дви-жуш,ейся вместе с жидкостью, т. е. на любой жидкой поверхности..

Требование найти решение уравнения (VH. 2. 3), удовлетворя-юш,ее условию (УП. 2. 2), представляет собой задачу Коши для линейного однородного уравнения в частных производных первого порядка.

Система обыкновенных дифференциальных уравнений, соответствующая уравнению (УП. 2. 3), имеет вид [1]:

= = = - (УП 2 5%

и V W т \ • • Г

причем и, V, W - известные функции координат и времени, так как потенциал скорости Ф задай. Ряд частных случаев рассмотрен Мас-кетом [Лт. I. 11), а также в ряде других работ (Лт. I. 8, 12, 19; Лт. П.. 2; 2, 24, 39, 40].

§ 3. Расчет скорости вытеснения одной жидкости другой из трубок тока, предполагаемых неизменными

Мы уже видели, что в общем случае - иенрямолинейного и ие-радиального течений - линии тока на границе раздела двух жидкостей испытывают преломление. Можно мысленно построить систему

Пусть надо найти уравнение жидкой новерхиости F {х, у, Z, t) = Q при начальном условии

/•(X, г/, Z, 0) = /(х, г/, Z), (УП.2.2) где / (х, у, z) - известная функция.

Проекции неремеш,ения жидкой частицы за время 61 будут

Ы, -bt, -Ы, где и, V, W - проекции скорости фильтрации

трубок тока В областях, занятых движуп;имися жидкостями. На границе раздела каждая трубка тока будет иметь излом, перемещающийся вместе с этой границей по мере вытеснения одной жидкости другой. Таким образом, весь процесс течения можно рассматривать как вытеснение одной жидкости другой из системы деформируемых трубок тока, сечения которых изменяются в зависимости от времени.

Заменим теперь эту истинную картину течения другой, физически заведомо неверной картиной. Предположим, что за все время движения

остается неизменной картина Pi Р2 линий тока, существовавшая

в начальный момент t = 0.

Тогда задача сводится к расчету времени вытеснения одной жидкости другой из системы трубок переменного по длине сечения, когда все эти трубки являются уже жесткими, недеформи-руемыми.

Рассмотрим какую-либо трубку тока переменного сечения (рис. VII. 2). Пусть площадь ее поперечного сечения есть функция длины &, отсчитываемой вдоль оси. Будем считать, что скорости фильтрации во всех точках сечения / = f (s) одинаковы.

Массовыми силами для простоты будем пренебрегать. Заметим попутно, что учет гравитационного эффекта, т. е. различия плотностей, не вносит никаких принципиальных затруднений, и, как правило, дает небольшую поправку. Из закона Дарси для расхода д, считая жидкости несжимаемыми, имеем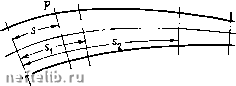

Рис. VII. 2.

к dp

Х ds

(VII. 3.1)

Предположим, что известны давления pi и в сечениях s = и s = S2. Выразим д через pi и р. Для этого из (VII. 3.1) найдем

~Г f

dp =

откуда, интегрируя и замечая, что д не зависит от s, получаем

Pi - Pi =

Pi -Р2

(VII. 3.2)