Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 [ 33 ] 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131

Внутри ЭТОГО контура размещено множество кружочков, являющихся проекциями скважин (рис. IV. 1, б).

На скважинах радиусами Гс устанавливается забойное давление Ро и соответственно забойный потенциал Фс.

Величины Рс будут зависеть от дебита и дебит - от величин забойных давлений.

Если Рс равно Рк, то никакого притока нет. Статический уровень всюду один и тот НхС и равен pjy. Если к скважинам начнется приток, то образуется разность давлений /?„ - рс - депрессия, под действием которой жидкость будет притекать к скважинам.

Для решения обратимся к формуле (I. 2.18)

ф = -Х1пг--const (IV. 1.1)

и поставим задачу о притоке не к одному, а к множеству точечных стоков или источников на плоскости, q = Qlh - дебит, отнесенный к единице мощности пласта.

Рассмотрим неограниченную плоскость и разместим на этой плоскости произвольное количество стоков или источников. Важно подчеркнуть, что вначале берется именно неограниченная плоскость, не ограниченный в плане пласт.

При линейном законе фильтрации и наличии нескольких стоков вызванные ими потенциалы можно алгебраически суммировать. Потенциал результирующего течения будет равняться алгебраической сумме потенциалов, вызванных каждым стоком в отдельности. Это называется принципом суперпозиции или сложения течений и следует из линейности уравнения Лапласа для потенциала и возможности суммирования его частных решений. Скорости течения при этом складываются геометрически, как векторы.

Возьмем произвольную точку пласта М (рис. IV. 2), в котором расположено множество стоков с дебитами q\, qi, ...

Можно, пользуясь принципом сложения течений, найти резуль-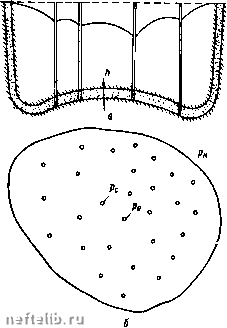

Рис. IV. 1. Схема притока к скважинам при напорном режиме.

тирующий потенциал точки М, суммируя потенциалы, определяемые формулой (IV. 1. 1):

1пГп + Сп), (IV. 1.2)

где п, Г2, Гз, ... -соответственно расстояния точки М от первого, второго, третьего и т. д. стоков; Ci, Сг, Сз, ... - постоянные (const), входящие в формулу (IV. 1. 1), различ- д ные для каждого стока.

От каждого стока будет своя собственная константа. Если их сложить, то получим одну суммарную константу. Таким образом, потенциал любой точки пласта можно представить в виде

Ф = 2 gilnn-bC, (IV. 1.3)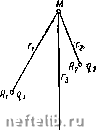

Рис. IV. 2. Qi

где п - число стоков; ri - расстояние от t-ro стока до точки, где определяется потенциал. При этом

С Ci + C2 + . . . + Сп= Ci-, ?i = , (IV. 1. 4)

1=1 "

где Qi - дебит t-й скважины со всей мощности пласта h.

Повторяем еще раз - пласт предполагается неограниченным в плане. При этом на бесконечности получается бесконечный потенциал.

В центрах стоков (г = 0) получаются также бесконечные потенциалы.

§ 2. Приток к совершенной скважине в пласте с прямолинейным контуром питания. Метод отражения

Формула (IV. 1. 3) является основной в решении задачи интерференции скважин.

Покажем применение этой формулы в двух случаях - для пласта с прямолинейным контуром питания и пласта с произвольным контуром питания, но удаленным от скважин.

В реальных условиях приходится встречаться не с бесконечным в плане пластом, а с площадью, ограниченной более или менее удаленным контуром.

Некоторые точные решения помимо приведенных в главе П1 могут быть получены при помощи известного в гидродинамике метода отражения.

Этот метод можно продемонстрировать на следующей задаче.

Пусть жидкость притекает к одной скважине, расположенной в полубесконечном пласте. Примем ось х за контур питания. На прямой у = О - оси X - поддерживается постоянный потенциал Ф„ (рис. IV. 3).

На скважине поддерживается другой потенциал Фр.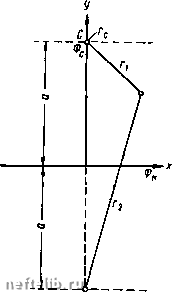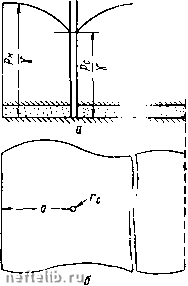

Рис. IV. 3.

Рис. IV. 4. Воронка депрессии при притоке к скважине в пласте с прямолинейным контуром питания.

Например, пусть в полосообразном нефтяном пласте пробурена одна скважина (рис. IV. 4, а). Тогда в плане (рис. IV. 4, б) будет пласт весьма большой протяженности с прямолинейной границей, на которой известны давление рк, и проекция единичной скважины радиусом Гс с забойным давлением рс.

Решим задачу о притоке к такой скважине.

Отличие от ранее рассмотренной задачи радиального движения заключается в том, что там контур питания был окружностью и пласт имел в плане форму круга, а сейчас пласт является полуплоскостью у О с прямолинейным контуром питания у = О - осью х.

Если бы пласт был неограниченным и в нем была единственная