Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 [ 66 ] 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131

откуда

Юн = 7 + (YB - Yh) sin а, (VII. 7. 8)

где = Цн/Цв - отношение вязкости нефти Цн к вязкости воды Цв. Для точки В

Юв + Уз sin а = ii5-f + у„ sin а,

откуда

(в\ = -- - (YB - Yh) Sin а. (VII. 7. 9)

Приув = Yh уравнения (VII. 7. 8) и (VII. 7. 9) совпадают с уравнениями, полученными другим путем А. М. Пирвердяном [16]. Расчетная схема А. М. Пирвердяна соответствует условию ку = оо [16].

Для радиального движения аналогичный результат был получен в [15, 16].

контакта и с увеличением согласно (VII. 7. 7) Aw увеличивается. Когда Aw > О, движение неустойчиво и язык нодошвенной воды будет двигаться гораздо быстрее.

Можно показать, что неустойчивое движение будет происходить по расчетной схеме ку = оо, изложенной в работах [15, 16].

Рассмотрим для этого движение граничных точек А п В (рис. VII. 13) вдоль кровли и подошвы наклонного пласта. Последовательные положения этих точек обозначены Ад, Ai, Bq, Bl, ... Для простоты проницаемость и мощность пласта к, h полагаем постоянными, а движение прямолинейно-поступательным с расходом q на единицу ширины. Поперечное сечение пласта в точке А проходит только через водоносную часть пласта, причем скорости частиц воды в этом сечении А можно считать равномерно распределенными. Аналогично в сечении В в нефтеносной части пласта скорости частиц нефти также будем считать равномерно распределенными.

Тогда из уравнения (VII. 7. 4), в котором полагаем {ki)2 = к = = к. Ух = ув, уа ~ ув (ув, у в - объемный вес соответственно воды

и нефти), = sin а, считая жидкости несн<имаемыми, получим

следующее.

Для точки А

f Х+ Y3Sma = J(u;J-bYsina,

Таким образом, согласно (VII. 7. 8) и (VII. 7. 9) при неустойчивом движении границы раздела скорости граничных точек А тл В (рис. VII. 13) вдоль кровли и подошвы пласта не совпадают со средней скоростью движения q/mh, где т - пористость. Точка А вдоль кровли при у в = ун движется в Ро раз медленнее, точка же В вдоль подошвы в Ро Рз быстрее.

При неустойчивом движении, когда темп вытеснения достаточен, различие объемных весов Ау = ув -унт О мало сказывается на этом результате. Более существенным фактором оказывается неполнота вытеснения, обусловленная фазовыми проницаемостями вытесняющей и вытесняемой жидкостей. Этот вопрос рассмотрен в работах [15, 17, 18].

Другие исследования этой задачи, основанные на методах, применяемых в теории гидродинамической устойчивости, приведены в работах [19, 20].

Устойчивое движение с достаточной точностью можно рассчитывать но схеме послойного движения частиц параллельно кровле и подошве пласта или но схеме жестких трубок тока.

§ 8. Конус подошвенной воды. Усчовия равновесия и прорыва подошвенной воды или верхнего газа в скважину

в тех случаях, когда площадь водо-нефтяного контакта очень велика, с самого начала эксплуатации скважины оказываются в нефтяном пласте с подошвенной водой (рис. VII. 14). Это имеет место в пологопадающих пластах

с очень малым 5тлом наклона к горизонту.

При отборе нефти поверхность водо-нефтяного контакта деформируется и принимает вид холма. Такой водяной холм называется конусом подошвенной воды.

Если повысить депрессию и отбор нефти, то вода прорвется в скважину и скважина будет давать нефть вместе с водой.

Точной теории водяного конуса до сего времени не имеется ввиду чрезвычайной сложности задачи.

Приближенная теория, позволяющая рассчитать предельный безводный дебит и форм> конуса, была предложена Маскетом [Лт. I. И], а также автором [21, 22].

Ниже кратко изложены физическая сторона явления и метод расчета, позволяющий определить пределы, между которыми заключен максимально возможный безводный дебит нефтяной скважины.

Расчеты показывают, что безводный дебит в однородных маломошдых пластах очень мал. Тем не менее даже в этих маломощных пластах скважины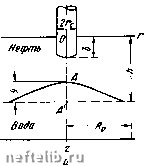

Рис. VII. 14.

дают иногда довольно большой нефтяной дебит без воды, хотя известно, что под нию1 имеется подопшепная вода. Это обстоятельство объясняется наличием непропицаемых или малопропицаемых пропластков, которые затрудняют вертикальное движение воды.

Рассмотрим сначала задачу о притоке нефти к несовершенной скважине при устойчивом неподвижном конусе подошвенной воды.

Пласт будем считать изотропным. Будем считать кровлю, подошву и первоначальный водораздел горизонтальными. Предположим, что водяной конус неподвижен и устойчив и к скважине притекает чистая нефть.

Направим оси координат так, как показано на рис. VII. 14.

Обозначим нефтеносную мощность через h, глубину вскрытия - Ь, радиус скважины - Гс.

В точной постановке требуется решить уравнение Лапласа для потенциала у2ф = о при следующих граничных условиях: кровля пласта непроницаема; поверхность водо-нефтяного контакта, форма которой неизвестна и сама подлежит определению, также пепропицаема для нефти. Основная сложность такой задачи заключается в том, что форма границы раздела воды и нефти, т. е. форма конуса, неизвестна. Таким образом, помимо трудностей, связанных с решением уравнения Лапласа, неизвестна область, в которой это решение должно быть найдено.

Предварительно выясним условия, при которых частицы воды на вершине конуса будут неподвижны.

Предполончим, что распределение давления в любой точке пласта известно, т. е. известна функция р = р (г, г).

Это давление в разных точках будет разное. Самое меньшее давление будет на стенке скважины.

Выделим на вершине конуса, т. е. в точке, лежащей на оси скважины, г = О, элементарный вертикальный цилиндрик пористой среды площадью df, высотой dz, заполпенный водой, и рассмотрим силы, которые на него действуют (рис. VII. 14, б), предполагая, что этот цилиндрик попал в нефтяную часть.

Пусть давление на верхнюю грань будет р (О, г) = р, давление на нижнюю 1рань р. Очевидно,

р=р(0, z-}dz) = p + - dz.

Составим уравнение равновесия нашей частицы воды. Сила, которая влечет эту частицу вверх, равняется

т(р--p)df = m dzdf, dz

где т - пористость. При этом нужно учесть, что жидкость занимает не всю площадь df, а только ее часть mdf. Вниз частицу воды влечет ее собственный вес, равный Yb mdfdz, где Yb - объемный вес воды.

Вопрос, будет ли частица воды увлечена вверх или не будет, решается сопоставлением этих двух сил.

Условие устойчивости частицы воды, таким образом, имеет вид:

ysmdfdz > т dzdf

Ув>- (VII. 8.1)

Условие (VII. 8.1) можно выразить, перейдя от давления к потенциалу Ф:

Ф = -(р±\н2),