Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 [ 72 ] 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131

Рассмотрим движение границы раздела в наклонном пласте мощностью h Угол наклона пласта к горизонту а (рис. VII. 28). Предположим, что жидкость 1 (вода) вытесняет жидкость 2 (нефть).

По-видимому, схема ку = со ближе к действительности в случае полого-падающих пластов, когда длина водо-нефтяного контакта гораздо больше мощности пласта h.

Выведем дифференциальные соотношения для границы раздела в предположении, что ку = оо (все уравнения выписываются для единицы ширины потока). Очевидно, что эта схема соответствует случаю, когда компоненты скорости, перйендикулярные подошве пласта, равны нулю, а параллельные распределены равномерно по сечению потока.

Отметим сходство и различие этой схемы со схемой ку = 0: при схеме ку = 0 перпендикулярные напластованию скорости отсутствуют, как и в схеме ку - со, но зато горизонтальные компоненты, вообще говоря, распределены неравномерно. Распределение компонентов скорости, параллельных напластованию, определяется из граничных условий для каждой трубки тока.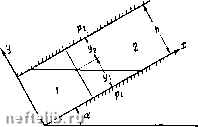

Рис. VII. 28.

Согласно уравнению Дарси имеем (рис. VII. 28)

91 =

92 =

А/ dz, р, [ ~

дрг дх

г/1.

г/г.

(VII. 10. 1)

где Ри Рг -давление соответственно на подошве и на кровле; у,, i/j -мощности, занятые соответственно жидкостями 1 и 2 (рис. VII. 28).

Составляя баланс расхода в предположении, что вытеснение поршневое (полное), и считая обе жидкости несжимаемыми, получаем

дУ1 dt

9дг дх

дУг dt

(VII. 10. 2)

Так как (рис. VII. 28) Pi = p2--Yi 2/i cos а--уг г/г cosa, то

дрг OPi dx dx

dyi dx

cos a.

Из рис. VII. 28 следует, что так как Ух-У2=-К то ду1 Эу2 dyi дуг

откуда

Ay cos a

дУ1 dx

AY = Yi-Y2-Из (VII. 10. 2) на основании (VII. 10. 3) имеем

(VII. 10. 3)

(VII. 10.4) (VII. 10. 5).

т. е. суммарный расход ?=gi+?2 = ?(0 зависит только от времени:

g = g(t).

Подставляя (VII. 10.4) в (VII. 10.1), получаем

hVi ( dPi

(VII. 10.6)

9i =

- Yi sin a

так как

--Aycosa- + YaSinaj , (VII. IQ. 7)

= sm a.

В дальнейшем будем рассматривать только горизонтальные пласты, т. е. будем полагать а = 0.

Складывая правые и левые части формул (VII. 10. 7) и учитывая (VII. 10. 6), получаем

9i + 92 = ?W =

9У1 дх

откуда

g(t)-JAyy

Hi Ц2

Подставляя (VII. 10.8) в (VII. 10.1) и (VII. IQ. 2), получаем

9i =

,(t)-J Ау KVi И2 дх

Hi дх

2У2 [4

Ц2 ду1 дх

klVl I 2У2

(VII. 10. 8)

(VII. 10. 9)

(VII. 10. 10)

i i i i i iu { и

1 f >/

11)} >nii 1 п п t п 11 } 11

Очевидно, что (VII. 10. 10) представляет собой дифференциальное уравнение относительно у\, так как Уг = h - yi. При ДуО это будет уравнение параболического типа. Случай ди)фО, Ду - О, когда II. 10.

10) обращается в уравне-

Рис. VII. 29.

ние первого порядка, рассмотрен А. М. Пирвердяном [16] и в работе [15]. Некоторые автомодельные решения для общего случая g{t) фО, Ау фО приведены в § И настоящей главы.

Рассмотрим представляющую самостоятельный интерес задачу о выравнивании возмущенной поверхности раздела под действием гравитационных сил (рис. VII. 29). При этом будем предполагать, что суммарный расход отсутствует: д {t) =0. Пусть в начальный момент форма границы раздела известна:

г = 0, 2/1 = !, = !,(х,0) = /(х). (VII. 10. И)

Уравнение (VII.IO. Ю) принимает вид при q{t) = 0:

CjCj Ay д

m дх I cy+Ciih-y)

ду dt

Ci=-

C2 =

Pi • \H

Введем аналогичную функции Лейбензона функцию ш (у):

,ilh 7/1

dy.

y{h-y)

Из (VII. Ю. 14) следует

д(а da ду у {h-у) ду

~дх~ dy ~дх~ Ciy-\-C2(h-y) дх

да da ду у jh-y) ду

(VII. 10. 12) (VII. 10.13)

(VII. 10. 14)

dy dt Cijz-hcj (ft -у) dt

и (VII. 10. 14) можно нереписать в виде

ссАу да ~дГ т дх

da dy

CiCgAy y(h~y)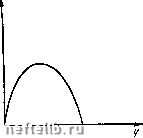

Рис VII. 30.

52(0

m Ciy + Ciih-y) dxi ~ dt Из (VII. 10.14) следует, что o) = o)(j/). Вводя обозначение c-ic Ay y{h-y)

m ciy-\-c(h-y) перепишем (VII.IO. 15) в виде

52(0

= x(2/) = x[!/((0)],

(VII. 10. 15)

(VII.IO. 16)

(VII.IO. 17)

Мы получили уравнение теплопроводности с переменным коэффициентом температуропроводности.

Характер функции х {у) представлен на рис. VII. 30. Если в (VII. 10. 17) заменить х (у) на его максимальное значение Хщах я толковать а как температуру, то, очевидно, это будет соответствовать более быстрому выравниванию температуры.

Верхний предел скорости выравнивания целесообразно рассчитывать по максимальному значению [х (у)]тзх-

Исследуя х{у) на максимум, после простых вычислений получаем

[х(2/)]тах = х = Jf (/-/)». (VII. 10. 18)