Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 [ 42 ] 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131

Однако, имея график для коэффициента совершенства т), можно рассчитать соответствующее значение С.

Из формул (V. 2. 8), (V. 2. 9) и (V. 2. 10) следует

т1 =

Решая последнее уравнение, получаем

lhn°

(V.2. 12)

(V.2.13)

Имея графики коэффициента т) и зная, для какого радиуса i? пласта они построены, можно использовать их для правильной методики расчета.

Фильтрационное сопротивление С, обусловленное несовершенством скважины или, что то же, ее приведенный радиус Гс, как указывалось, практически не зависит от расстояния между скважинами, когда оно равно или больше

мощности пласта. Если же расстояние между скважинами меньше мощности пласта (такие случаи близкого расположения скважин встречаются иногда в горнорудных и гидротехнических задачах, связанных с осушением предназначенных для разработки пластов полезных ископаемых или водопонижением [17]), то С зависит также от расстояния между скважинами. Этим вопросам посвящены работы Л. И. Павловской [18] и И. Н. Кочиной [19].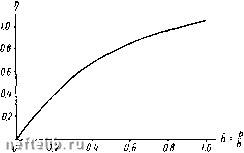

Рис. V. 8. График коэффициента совершенства.

§ 3. Расчет фильтрационного сопротивления, обусловленного несовершенством скважины в однородно-анизотропном пласте

Как известно, простым преобразованием масштабов движение в условиях однородно-анизотропного пласта может быть сведено к движению в однородном пласте.

В однородно-анизотропном пласте горизонтальные и, г; и вертикальная W проекции скорости фильтрации имеют вид:

кт др кг др kz др

\1 ду

и = -

р дх

р dz

(V. 3.1)

Введем в рассмотрение Ф - фильтрационный потенциал, определяемый по горизонтальной проницаемости. Тогда вместо (V. 3. 2) получим

Заменой переменного xz = z уравнение (V. 3.3) обращается в уравнение Лапласа

а2ф dФ агф

+ + = (V.3.4)

Рассмотрим теперь следующую задачу.

Найдем распределение потенциала в однородно-анозотропном пласте мощностью Л, вскрытом скважиной, при следующих условиях. Условия непроницаемости кровли и подошвы

г = 0, z = A, (rc<r<i?o), -- = 0; (V.3.5)

на области питания

r = i?o, (0<z<fe) Ф = Фо; (V.3.6)

на стенке скважины г = Гс задан неременный расход на единицу длины вдоль оси скважины-стока:

г==ге, (2яг-Ц = д(г) (0<z<;j). (V.3.7)

Вид функции q (z) может быть произвольным с единственным ограничением - предполагается, что q (z) удовлетворяет условиям Дирихле [Лт. HI. 7].

Решение уравнения Лапласа (V. 3. 4) получается обычным методом разделения переменных. Рассмотрим сначала случай однородно-изотропного пласта, когда х = 1, z = z.

В силу симметрии уравнение Лапласа в цилиндрических координатах имеет вид:

dФ ,i9ФdФ .

-а + УаГ + -а = 0. (V.3.8)

и решение его не будет зависеть от полярного угла 9.

где кт - проницаемость в направлении параллельно пласту; kz - проницаемость в направлении оси z перпендикулярно пласту.

Считая жидкость несжимаемой, из уравнения неразрывности

ди , dv , dw ~

% + air + "5Г = о получаем

*te + S-)+feS = 0. (V.3.2)

Решение уравнения (V.3.8) будем искать в виде

0 = i?{r)Z(z), (V.3.9)

где R (г), Z (z) - неизвестные пока функции, зависящие соответственно от аргументов г и z.

Подставляя (V. 3.9) в (V. 3.8), получаем

Z (i?" 4- Д) + i?Z" = О

= + = ±х2. (V.3.10)

Поскольку левая и правая части (V.3.10) зависят только от одной переменной - соответственно z, г, равенство (V. 3.10) мсЖет выполняться тождественно только при условии, что левая и правая части равны постоянной величине ± Л., которая предполагается вещественной.

Уравнение (V. 3. 10) расщепляется на два уравнения:

Z"±%Z(d, (V.3.11)

/?"+ (V.3.12)

Если в (V. 3-10) при А, стоит знак минус, то линейно независимые решения уравнений {V. 3. И) и (V. 3.12) имеют вид:

Z = e-\e\ RJo{%r), Yi-Kr), (V.3.13)

гдо 7o, Yo - функции Бесселя соответственно первого и второго рода нулевого порядка вещественного аргумента.

Если в (V. 3.10) ири Л. стоит знак плюс, то линейно независимые решения уравнений (V. 3.11) и (V. 3.12) суть

Z = sin Az, cosAz; R = Io(lr), Ko{Xr). (V. 3.14)

где Io, Ко - функции Бес селя первого и второго рода нулевого порядка мнимого аргумента [20]. При А = О

Z = ciz 4- С2, Я = Сз hi г -Ь С4. (V. 3.15)

Так как при z = О согласно граничным условиям должно быть = О, то решения (V. 3.13), а следовательно, и знак минус отпадают. Этому же Граничному условию из решений (V. 3.14) удовлетворяет только функция cos К Z. Для выполнения условий на