Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 [ 4 ] 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284

1.5.3.1.2. Относительное движение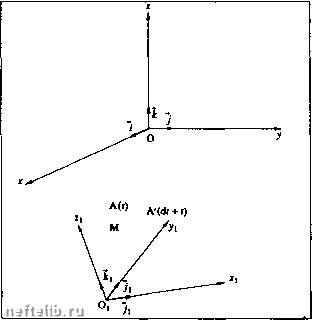

Очевидность только кажущаяся. На самом деле, следующие ниже теоремы вытекают из принципа универсгтьности времени, примененного к различным системам отсчета.

Система отсчета О предполагается неподвижной, а система отсчета О - подвижной.

Пример: парковый аттракцион, состоящий из вращающейся платформы и подвижных стрел, на концах которых закреплено по самолету.

Oxyz- площадь в парке,

0,Xi/,Zi - платформа, она вращается (скорость переменная),

А - ребенок, сидящий в самолете (круговое переменное движение).

Будем рассматривать:

- точку пространства М, фиксированную относительно OiXi/,Zi и совпадающую с А только в момент f,

- вектор OiM фиксированной длины (на твердой платформе)

- и ОМ = Об, + OiM.

1.5.3.1.2.1. Анализ скоростей

1.5.3.1.2.1.1. Переносная скорость (скорость платформы относительно земли)

~dr- -dГ~dГ• Зaмeчaниe; Плaтфopмa вращается. О, - какая-либо фиксированная точка на оси вращения:

dO,M

- вращательная составляющая М;

dO.M г

= ПлО,М = ПлОр

П - угловая скорость вращения любой точки платформы.

Платформа не совершает поступательного дви-

ЖбНИЯ и

= о.

но в общем случае:

есть скорость поступательного движения

(система отсчета перемещается параллельно сама себе); кроме того, в общем случае П не имеет постоянного направления.

1.5.3.1.2.1.2. Относительная скорость Скорость самолета относительно платформы:

V,= {-) в системе Oxyz

or о,

ДА мЛ-мЛ (УМА

dt dt dt

Вектор аА" не зависит от системы отсчета.

1.5.3.1.2.1.3. Абсолютная скорость (относительно земли)

dt dt * dt Теорема сложения скоростей:

1.5.3.1.2.2. Произвольный вектор Аб

"Относительная" производная вектора

Неважно, что представляет вектор Аб (сила и т.д.):

Аб = бб-бД С другой стороны,

dOA d66, s dO

dt о dt о dt о,

и так же для 65. Отсюда теоремы:

dt о of о,

в частности

da da dt о dt о,

1.5.3.1.2.3. Разложение ускорений

Для правильной идентификации слагаемых в сложном выражении, которое будет выписано ниже, заметим, что относительное ускорение - это. очевидно,

к df Jo V df /о.

и что в случае, когда оно и относительная скорость обращаются в ноль, остается только переносное движение.

Отделяя поступательную часть переносного

движения (скорость (

сЮб,

абсолютной скорости, получим:

. ) ) в выражении для dt о

- сЮб,

QaO,A-(-(--1-) at о,

С помощью предшествующих теорем находим далее:

(d06,

V dt

-ь[(йло;1)о-ь

т.е.

d6Q,\

1У dt

+ ( -) лО,А +

ОГ о

Теорема ускорений:

У, = % + Уг + Ус

где % = 2Q л V, есть ускорение Кориолиса.

1.5.3.1.2.4. Основной принцип динамики

в произвольной системе отсчета

Если система отсчета Oxyz инерциальна, то для наблюдателя, находящегося в системе 0,x,/,z„ закон динамики принимает вид

где - rrifg - переносная сила инерции, - nffc - кориолисова сила инерции. Замечание:

Можно рассматривать - nffr как силу инерции в системе О, (принцип Даламбера).

1.5.3.1.3. Другие записи закона

для материальной точки

1.5.3.1.3.1. Количество движения

Если обозначить mV= Д количество движения,

то Р = (в инерциальной системе отсчета), Tdt dt

называется импульсом (элементарным).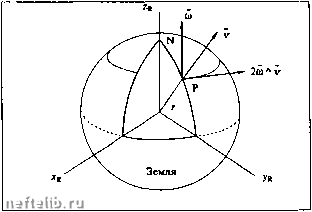

Пример кориолисова ускорения во вращающейся системе координат: вращающаяся система (xpyZfj) фиксирована на Земле; параллельно zp. Предмет, брошенный вертикально вверх из точки Р на поверхности Земли, имеет начальную скорость V. Кориолисово ускорение 2(Sл v направлено по касательной к параллели, как показано на рисунке; N -северный полюс. Если бы предмет свободно падал с некоторой высоты над поверхностью Земли, кориолисово ускорение имело бы противоположное направление.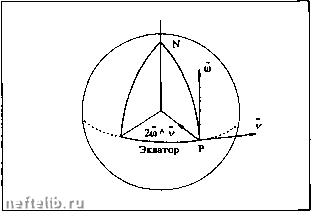

Другой пример кориолисова ускорения: ли предмет Р, находящийся на экваюрв, имеет скорость v (относительно поверхности Земли), направленную по касательной к экватору, то, в дополнение к ускорению силы тяжести, он будет испытывать направленное к центру Земли ускорение величины 2т.

1.5.3.1.3.2. Кинетический момент

Пусть О - фиксированная точка, М - материальная точка. Обозначим ОМ л р = 9о кинетический момент; имеем:

1.5.3.1.3.3. Кинетическая энергия Если М смещается на ис/f, то:

Р • vd/ = • vdf = d(mv) = dE = cfigp,

увеличение кинетической энергии равно работе силы Р.

1.5.3.2. Материальная система

Из принципа действия и противодействия [Pj = О вытекает, что торсор внутренних сил системы равен нулю.

1.5.3.2.1. Центр тяжести,

или центр инерции, или барицентр

G таково, что 5m,GM, = О или MOS = 5трм„ VO, где М = т, = полная масса системы.

1.5.3.2.2. Теорема

о движении центра инерции

Дифференцируя, имеем: MVq = т,

откуда:

-dT---dt-

Центр инерции системы движется так, как движется точка, имеющая полную массу системы, под действием результирующей внешних сил.

1.5.3.2.3. Теорема о кинетическом моменте

0 = 2:ОМ,лт,7„

где О фиксировано в инерциальной системе, следовательно:

Эта теорема касается "вращательного" аспекта движения системы.

1.5.3.2.4. Теорема о кинетическом моменте относительно G

Од = 5об л тр, + GM, л тр,. Зо = мой л Vq + 5q -1 -ая теорема Кенига.

= 05лМ-+ -,

откуда

Эта теорема характеризует движение вокруг центра тяжести, т.е. по отношению к барицентри-

ческой неинерциальной системе отсчета: оси проходят через G и остаются параллельными самим себе.

1.5.3.2.5. Теорема кинетической энергии

dig, = P,v,dt = т,- v,dt = d(-m,\),

откуда:

Увеличение кинетической энергии системы равно сумме работ внешних и внутренних сил (всех сил, приложенных к системе).

В неинерциальной системе (скорости 7/вычислены в неинерциальной системе) надо учитывать работу перенорных сил инерции; кориолисовасила инерции - 2mQ л всегда перпендикулярная движению, не работает; поэтому для каждой точки имеем:

F, -"РуВ -,с = т,

dV, dt

(F-"P,e) • W,dt=mp. dV, dig,,+ dig,, = d(lm,Vb,

что следует просуммировать по всем точкам, полагая rfKj, = -FV,* - работа переносных сил инерции.

Различают работу обратимых внутренних сил и работу внутренних сил трения, т.к. последние всегда направлены противоположно создающему их движению. Эта работа отрицательна; она рассеивается в тепло.

1.5.3.2.6. 2-ая теорема Кенига

Если подвижная система отсчета барицент-рична (движется поступательно, оси проходят через G), то:

Кинетическая энергия системы равна кинетической энергии поступательного движения полной массы, увеличенной на кинетическую энергию движения вокруг центра массы.

1.5.3.2.7. Теорема мощностей

Мощность определяется как W = -- (работа в единицу времени), поэтому

= кинетическая мощность.