Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 [ 21 ] 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108

т. е. коэффициент затухания волн первого рода пропорционален квадрату частоты колебаний. Выражение (8.14) можно непосредственно получить из формулы (7.11), если совершить в последней предельный переход к мягким средам.

Заметим, что характеристики продольных волн первого рода в мягких средах не зависят от упругих модулей переупаковки твердых частиц Я,2, а определяются только сжимаемостью фаз Р, Рг и величиной пористости т. Однако продольные волны второго рода (как и поперечные волны) в мягких средах будут характеризоваться только параметрами Ji, Jij а не Р, Ра- Покажем это.

Для продольных волн второго рода справедливо следующее исходное соотношение:

Й=1-Г, (8.15)

которое для волн, бегущих в положительном направлении оси х (в пренебрежении величинами порядка малости и выше), можно представить в виде

(8.16)

Скорость распространения волны второго рода г определится по формуле

УЖ (V 1+1 + 1) • (8-17)

Отсюда следуют два предельных выражения

Уб-с = (5р)-/. нри-оо,

при 0.

Коэффициент затухания для волн второго рода имеет вид

(8.18)

и соответственно б О при оо, б(, оо при S -> О и при фиксированном со, тогда как при фиксированном параметре paj\i, при со ~

О имеем 6 О, а при со оо

6.-4

2 ао

(8.19)

Результаты расчетов по формуле (8.17) представлены на рис. 8.

Из приведенного здесь анализа следует, что величины Vj, и б, обращаются в нуль (при некоторых значениях параметров среды и частоты) только в масштабе порядка единицы, так как, строго говоря, они могут быть величинами е малого порядка.

Результирующие формулы (8.17), (8.18) соответствуют упрощенной модели пористой среды, сложенной из несжимаемых фаз (Pi = = = 0) - см. [166].

При исследовании зависимости коэффициента затухания от частоты колебаний в волне удобно рассматривать связь безразмерной величины = (p4S/(lA5p) и 1 (рис. 9).

Значения параметра т = (PiPao) ((тоРо)"", характерного времени релаксации (запаздывания) механического процесса, происходящего при распространении волн, для некоторых водонасыщенных грунтов приведены в табл. 4.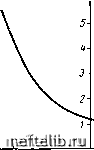

-Ч -3 -2 -1 О I 2 3 Ч 21п°

5 В 1

-5,0 -2,5

Рис. 8. Зависимость скорости yj, продольной монохроматической волны второго рода в мягкой насыщенной среде от частоты и параметров среды: (i;gBp)"i=

=/(о)ряоР"1).

Рис. 9. Зависимость коэффициента затухания продольной монохроматической волны второго рода в мягкой насыщенной среде от частоты коле-бзЕШЙ (при фиксированных параметрах среды).

С целью сравнительной оценки характерных скоростей v, vo я с приведем данные подсчета для кварцевого песка {т = 0,3, р = = 2,5 г1см, Рг = 1 г/см, = 2-10-в ат-\ Рг = 4-10-« ат-\ В = = 0,001 am-i).

i;(, = -==l,9 км/сек, г?„ = 77=-== 2,2 км/сек,

V Bp

0,14 км/сек

(8.20)

Для сейсмических волн в водонасыщенных грунтах параметр Z, = = Р(,сот/роо оказывается (см. табл. 4) весьма малым, и для волн первого рода будет справедливо асимптотическое выражение (8.14).

Для волн сейсмических частот второго рода в силу малости параметра при этом будет справедлива асимптотическая формула

-1У шрВ

(8.21)

Таблица 4

т. е. коэффициент затухания пропорционален корню квадратному из частоты со. Деление соотношения (8.21) на (8.14) приводит к следующему результату:

(8.22>

т. е. волне второго рода по сравнению с волной первого рода той же частоты свойственно неизмеримо большее затухание. Отсюда в насыщенных жидкостью грунтах практически могут распространяться: только волны первого рода. В то же время в сухих грунтах отсутствуют волны первого рода и распространяются только волны второго рода. Действительно, там (д, О, ра О, т. е. сю, -> О, iJft -> с; = 1 5pi. Таким образом, выше уровня грунтовых вод скорость распространения наблюдаемых сейсмических волн равна = 1/у 5pi, а ниже г; = г?о, определяемой по формуле (8.8). Отсюда скорость распространения наблюдаемых продольных волн при переходе через зеркало грунтовых вод возрастает в N раз, где

Щ К Ро К .Со

(8.23)

vb У ро

что и подтверждается рядом наблюдений [129, 304, 305].

Это дает также объяснение приведенным в табл. 3 данным о величинах скоростей наблюдаемых продольных и поперечных волн. Становится ясным, что в мягких средах уплотнение пористой среды, которое не приводит к нарушению условия ё С 1, заметно влияет на скорости и у;,, но пракилески не сказывается на скорости первой продольной волны Va- Поэтому соотношение между скоростями продольных и поперечных сейсмических волн в слабо сцементированных ненасыщенных пористых средах примерно одинаково, тогда как при полном насыщении среды капельной жидкостью это соотношение резко меняется. Подчеркнем, что в сильно Сцементированных средах скорость волны первого рода зависит также от коэффициентов Ламэ - см. формулу (7.10) - и увеличение степени сцементированности влияет на характер их распространения (см. § 10),

Рассмотрим подробнее механизм, определяющий дисперсию и затухание наблюдаемых продольных и поперечных волн в мягких насыщенных пористых средах.