Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 [ 46 ] 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108

поскольку pJ/p5 = Pi,(р - Ро)- С другой стороны, скорость слабой ударной волны, соответствующая равновесному состоянию В и определяемая формулой (17.22), оказывается равной f/=l/(Ppo). Таким образом, в слабой ударной волне стационарная структура фронта невозможна [311] - замороженное и равновесное состояния распространяются с заведомо неравными скоростями. Интенсивность размыва фронта слабой ударной волны и его трансформация в непрерывную волну давления оценивается с использованием акустических уравнений - см, соотношение (17,8). Предельное непрерывное решение построено Р. И. Нигматуллиным (см. Вестн. МГУ, серия «Математика, механика», 1969, № 4, стр. 122-126).

Для возмущения пористости имеем

т. е. в водонасыщенном кварцевом песке, где Ра > Р, пористость на слабом скачке давления возрастать не может.

В работе Я. 3. Клеймана [97] условия на сильном разрыве в многокомпонентной смеси, соответствующие уравнениям X. А. Рахматулина [186], формулировались на основе рассмотрения баланса сил и масс. При этом Я. 3. Клейман принимал, что на каждую фазу двухфазной среды действует сила, равная (1 - т) р и тр, и именно она фигурирует в уравнениях движения фаз. Это соответствует расчетной схеме Н. А. Слезкина [198] и Био [257], тогда как в уравнениях движения Я. И. Френкеля [215] (сводящихся при равенстве фазовых напряжений к уравнениям X. А. Рахматулина [186]) потенциалом действующих в жидкости сил служит само давление р.

Иа соотношений на разрыве Я. 3. Клеймана [97] для условий, аналогичных рассмотренным, следуют равенства массовых скоростей фаз и для сильных ударных волн. На самом же деле системе уравнений X. А. Рахматулина [186] соответствует именно равенство (17.24) и только для волн слабой интенсивности они совпадают.

Для оценки ширины стационарного релаксационного слоя ударной волны необходимо решить систему интегралов (17.7)-(17.9) и нелинейного дифференциального уравнения (17.11) при начальных условиях, определяемых соотношениями на фронте ударной волны (17.24)-(17.27), при S = 0. Из-за нелинейности системы приходится прибегать к численным методам, причем удобнее представить интегралы (17.17)-(17.19) также в виде дифференциальных соотношений

4 -До- dl~ Ао dl~ До dl~ Ао • (" где для удобства используются следующие безразмерные переменные:

Р = р2(р-Ро). P = Pi/p2, uuJU, W = WJU, р2 = рг/рг", Pi = Pi/P?,

=iS» ?=p"P• ~-{PWo, 0=-.

Р2 {Р)

- тпо--~ W -(1-mo)u•

Р2 [Р) Р2 (Р)

--\a-mo)Qu»+i[-m)]. Р2(Р) Ра I

Аз = <? {- i - rrio) ти - тпо (1 -те) Wj,

- - т(\-т) 9

Р2(Р)

(\-mn)uQp\

(1 + РН1р)р»

1 + х.2Р

(m) " 1 -f X2P 1 -f- pip

Начальные условия удобно определять следующим образом. По

задаваемому значению из кубического уравнения определяется величина Q. Здесь

В = 2/i (/з + /2) - 12/4/1 + 2 (/з + /2) - /з],

c={h + UY -2/4 (/3 + /2) + 2/4/3, D = /1/3,

(17.36)

/ 1-то 1 то р§

1 1-"о "о

/2 = /. 1-

«о

Р2 /

/3 = Ul+2Pj

1-1/-X

1], /4=-

Х2-1 V " Л

Затем по найденному значению Q определяются значения

Р2<А

(17.37)

1 -то

Pl Ил + ("0/Р2)

Пример расчета. Оценим ширину ударной волны в водонасыщенном кварцевом песке. Для этого положим: pj/pj = 2,65, р = 0,1, Р2 ~ 5-10"В ат-.

По данным работы [62} показатель xj, измеряемый на ударной адиабате для мрамора, принимает значеш1е xi = 7,23 до давления р = 1,5 Юв am, а при более высоких давлениях х, = 4,1. Примем в связи с этим для материала твердой фазы -лу = 7,23. Для воды можно принять xj = 7,00 [109].

Расчеты были выполнены также для Xj = Хо = 3 (поскольку в работе [135J ранее проводились оценки соотношений на фронте ударной волны как на простом разрыве именно для такпх значений параметров Xi, Х2) и для Xi = 3,96; Хг = = 7,00.

Начальные значения пористостп toq принимались равными 0,2; 0,3; 0,41. При изменениях пористости среды меняется также ее проницаемость и соответственно а (т) = «о (т/то)" (1 - т)/(1 - то)- Исходя из опытных данных Фатта [8], примем п = 10.

Для оценки коэффициента Ь (инерционных потерь) воспользуемся результатами известных экспериментальных исследований отклонений от закона Дарси, проведенных И. М. Жаворонковым,

М. Э. Аэровым и Н. И. Умником [8]. Указанные опытные данные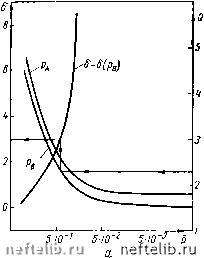

0,16

0,18

5W S-tO~ б

5-10

u,w -0,65

-0,10 -0,15 -0,80 -0,85 -0,90 -05

Рис. 13. Рассчитанные замороженная п равновесная ударные адиабаты н ширина фронта ударной волны (а), а также скорости частиц и пористость (б) для грунта начальной пористости: = 0,2 при = 3,00, х = 3,00.

представлены в виде функции / = / (Re) от числа Рейнольдса на рис. 3, причем

/(Re) = l +

mo (1-mo) ро

„), Re=f/ o рО. (17.38) Po Г mo(l -mol

Из графиков (рпс. 3) видно, что функция / (Re) = 1 для засыпки шариков пористости m я« 0,4 и проницаемости fc я« 3 -10 д при Re 0,4, а в диапазоне 1 Re 4 может быть приближена прямой линией

/(Re) = l + 0,35Re. (17.39)

Будем считать для простоты, что зависимость (17.39) справедлива при всех значениях числа Re О (что приводит к завьппению эффекта инерционных сил сопротивления для естественных пористых горных пород: fc я=; 1 5 и менее). Тогда сопоставление соотношений (17.37), (17.38) показывает, что

то (1 -то)

= 0,35.