Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 [ 78 ] 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108

Для области вдали от скважины Д > 1 решение (26.21), (26.22) еще больше упрощается

= - Ао RV

S2 (82ST+1)

st+ 1

(26.23)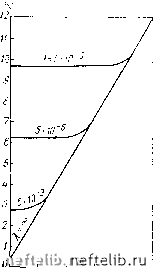

/0 ;0« rfff ro гй""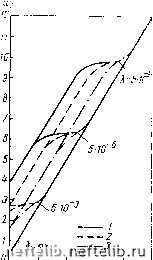

Рнс. 32. Завпсимость безразмерного давления (гд, <) от параметров Я = г/хт, со = 82 (1 -Ь 82)"1: а <о = 0; б: 7 и =0,001, 2-u) = o,01; з-а = 0,1.

и совпадает с решением для точечного источника в моменты времени < ~ т - см. формулы (26.18) - (26.19). Решение (26.23) было предложено в работе [324], причем для оригиналов было дано асимптотическое представление для безразмерного давления в трещинах на стенке скважины {R = 1):

хг-г

t 1-Ьег

t 2 J

(26.24)

где -Ei[ - z]=-\ -эксноненциальный логарифм.

Там же приведено решение для конечного кругового пласта с непроницаемыми внешними границами (при R = = R/,)

(26.25)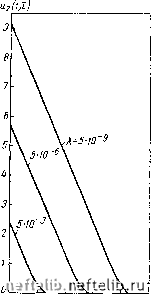

Ю" to* WfO w° jj-

U2(l,t) 3.5

Ь5 ЬО 0,5 О

Рпс. 33. Графики завпспмостн возмущения безразмерного давления 2 (г, t) от безразмерного временп

а - со = 0; б: 1 - o) = 0,1(01; 2 - to = 0,01; 3 - to = 0,1.

Для ряда имеющих практотеский смысл значений параметров Л = г/хт и (О = 62/(1 -Ь е) по приближенной формуле (26.24) были проведены расчеты. Графики зависимости безразмерного давления в трещинах на стенке скважины (г, t) от безразмерного времени хг/г§ приведены на рис. 32. На рис. 33 показаны графики зависимости возмущения (обусловленного конечным временем релаксации т) давления (г, t) от безразмерного времени.

Значение Х - соответствует мгновенному выравниванию давлений в первичных п вторичных порах: т = 0. В соответствии с общим анализом, проведенным в § 22, в условиях полного пренебрежения сжимаемостью спстемы трещин (82 = 0) возмущение и„ изменяется скачком прп t = О (волна давления в трещинах проходит мгновенно), а затем монотонно.

Из графиков рис. 32, а также видно, что кривая (т, t) выходит на прямую линию, соответствующую обьгано.му упругому режиму пласта примерно прп t = т.

Согласно данным рнс. 32, б начальное изменение давления обусловлено

отличным от нуля значением г причем примерно со значений xi/r--1 реше-

ние выходит на режгш, соответствующий условию 63 = 0 (см. рис. 32, а и 32, б).

Однако в реальных условиях характер изменения забойного давления после внезапного пуска может быть еще более сложным. В самом деле, согласно оценкам, приведенным в качестве npmiepa в книге [8] (стр. 161), раскрытию трещины в 0,1 мм соответствует ее эффективная проницаемость к = 830 д. Отсюда при пронпцаемостп блоков к = i; 10; 100 «9 имеем соответственно оценки Е = 10" 6 10"*. Сопоставление с принятыми в работе [324] значениями Хг я=г 5 (10" 8 -i- 10" ) говорит о ТОМ, ЧТО на забойном давлении в скважине в рассма-

/ xi 1 \

трпваемые интервалы временп I -т- - , > - s = s, А, ) будет

V г<. 81 X J

существенно сказываться наличие малой, но ненулевой проницаемости блоков.

Отметим в заключение развитые приближенные методы решения задач неустановившейся фильтрации в треш,иновато-пористых пластах - метод моментных соотношений и метод коллокаций. Следует подчеркнуть, однако, что применение здесь метода моментных соотношений, строго говоря, требует введения двух характерных зон изменення давления (см. стр. 205 - 208).

1 Э. А. Авакян. Некоторые приближенные решения задач фильтрации в трещиновато-пористой среде. Изв. АН СССР, серия «Механика жидкостей и газа», 1967, Л"» 4.