Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 [ 70 ] 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108

выполняется. Но, если аК О, второе условие (24.5) следует заменить, как это сделано для фильтрации газа в работе [14], на условия

и(У = 0, {l) =-ka, loO, Ка<0, (24.6)

то при 5 ?о имеем

и()-и(Ео) = -Яа1п(/Ео)

и условие u () О выполняется вблизи точки go- Переход к этому условию соответствует замене скважины пренебрежимо малого (но постоянного) радиуса на фиктивную скважину с расширяющимся радиусом г(. = loVKt, на стенках которой (при = f о) задают условие постоянного расхода q= -7м и условие постоянства давления.

Разберем метод построения численного решения указанных задач на примере наиболее сложного варианта - осесимметричной задачи при ак < 0. Задача формулируется следующем образом: требуется найти такие и (), q (1) я о> чтобы были удовлетворены уравнение (24.5), первое из условий (24.5) и условия (24.6).

Уравнение (24.5) эквивалентно следующей системе:

-Т • f = --°- (24.7)

Интегрируя второе из уравнений (24.7), получим

q (1) = хХ ехр I -/ u-°tdt) , (24.8)

а затем из первого уравнения (24.7) находим, что

со у \

u (g) = 1 + Ка J ехр I - J u-4dt j . (24.9)

Выберем величину = настолько большой, что при функции и() практически не отличается от единицы. Тогда из уравнений (24.8)-(24.9) получим

и ih) = 1 -Ь g (х) ехр (-f.) ( -f-) ,

4i ill) = -01. ехр -J u-tdt

(24.10)

Процесс построения численного решения системы (24.7) при указанных граничных условиях состоит в следующем. Сначала определяется решение системы (24.7) при а = О, причем считается, что условия и = О, (7 = -Яа выполняются в точке J = 0. Полученная

0,9 0.7 о.ь 0.3 0.

wo

0,1 0,8 1,2 1,0 2,0 2,4- г,61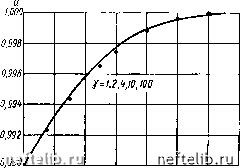

О.Ч 0,8 1,2 1,6 2,0 2/t 2,8 i

0,92

0,80

1,10

1,0д 1,06

1,04

1,02 1,00

0.8 1,2 1,0

2,0 /.lit.

Рис. 27. Сопоставление точных и приближенных решений уравнения (24.1) для линейной фильтрации при и (0):

а -0,10; 6-0,80; в-0,99: г-1,10.

- О 0,1* 0,8 1,2 1,6 2,0 2,4 2,8}

о 0,4 0,8 1,2 1,61

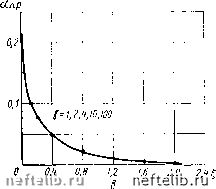
0 0" 0,8 1,2 16 2,0 2.4 2,8 i, 5

Рис. 28. Сопоставление точных и приближенных решений уравнения (24.1) для осесимметричной фильтрации при аЯ > 0:

а-0,01; 6-0,10; в-0,05.