Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 [ 35 ] 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108

р (х, t) =

Yz2-x2/c2

x/c

2/c2

0 арих>и1

Для жидкого поршня

: ct

о (х, г) =

-spsfh прп с/ < X О приг>1;г

при г ci

/z2 -x2/c2

Р (X, t) =

i д:/<;

прп г ci p*(l -е/г) при с/ < X sc ri 0 при г >i-i

/i (bft/z2-a:2/c2 /z2 -г2/с2

Для жесткого поршня

a (X, i) =

еГ/г при X s: i>i

P {X, t)

0 при x> vt

-r*(lJ-8/) npnxSCyi

0 при X > y/,

(13.20)

(13.21)

(13.22)

(13.23) (13.24)

имеем в этом

тогда как иа второй волне с точностью до членов порядка е случае [о] = [р] = 0.

На рпс. 12 представлены эпюры напряжений и давлений для этих трех случаев в фиксированный момент времени i при условии, что напряжения о,,, < О, У* < О (сжимающие), р*>-0.

Поскольку известны величины скачков на фронте первой и второй воли, а также значения коэффициента затухания, можно построить примерный вид эпюр напряжений и давлений при pi Ф рз (пунктир на рис. 12).

Другим частным случаем, для которого можно построить полное решение, является задача о слабом сжатии среды, составленной из несжимаемых фаз: Pl = Рг - 0. При этом I Яд I оо е О, т. е. слагаемые с интегралом Sa выпадают, п, кроме того, всюду существенно упрощаются выражения (s),

/777711

\0 df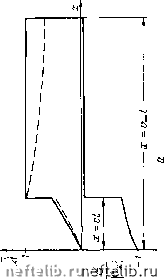

x = ct

Piic. 12. Эпюры дпнамичиского распределения давления и напряжения при сжатии мягкой насыщенной среды:

а - Высоьопроницасмым поршнем; б - !1;11дьим поршнем; в - жестким (непроницаемым) поршнем (сплошные линии р, Рг, нуинтир-ные р, ф Рг).