Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 [ 9 ] 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108

Соотношение q = к (Т - i) для описания осредненного межфазового перетока в сплошных гетерогенных средах было введено Л. И. Рубинштейном [193].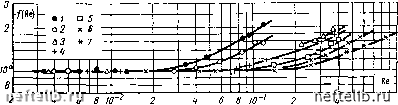

в в w-

Рпс. 2. Представленпе экспериментальных данных Фепчера, Льюиса и Бернса в виде / = / (Re):

Рис. 3. Представленпе экспериментальных данных Н. М. Жаво-ронкова, М. Э. Аэрова и Н. Н. Умника в виде / = / (Re):

Определенпе согласно условиям (4.27) внешних притоков тепла в фазы справедливо как примерная оценка, если в рассматриваемой фазе нет изолированных частиц. Примером таких фаз и являются жидкость и твердый скелет в насыщенных пористых средах. При нарушенцп этого условия необ.ходпмо-

прибегать к усложненным теориям обобщенной проводимости гетерогенных систем. Предельный пример такого рода нарушений - взвеси, где все твердые частицы оказываются взаимоизолированными (/Р = 0).

Интерпретация закона (4.27), определяющего силу Л,- для взвеси, связана с формулой Стокса (см. второе слагаемое справа уравнения (3.30)). Сопоставление уравнений (4.27) и (3.30) показывает, что «проницаемость» взвеси к = - (1/18) dm (1 - га)"1. Однако третье слагаемое правой части уравнения (3.30), отражающее нестационарность режима течения в микроканалах, не учитывается в (4.27). Как и следовало ожидать, методы существующей термодинамики необратимых процессов позволяют описать микростационарные процессы (см. § 11).

В связи с этим М. Био [260] вводит понятие вязкодинамического оператора Y (z), действие которого на величину относительной скорости фаз определяет результирующую силу межфазного взаимодействия

RiY (z)(wi-ui), г=

причем по м. Био оператор У (z) учитывает также эффект прпсоединеииой массы (см. первое слагаемое в правой части уравнения (3.30).

Суммирование уравнений (4.1) и (4.17), а также (4.15) и (4.16) шриводит к соотношениям Гиббса для жидкой и твердой фаз.

diEi

dt Р dt р2~ dt •

Поскольку средняя внутренняя энергия жидкости подчиняется -уравнению (4.29) - такому же, что и у свободной жидкости, - то можно предположить, что средняя энергия так же зависит от средних параметров состояния (Рг, или р, Т), как и локальная энергия Е\ (соответственно от локальных значений р, s или р, Т. Уравнение состояния жидкости определится соотношенпем

р=() . V, = - (4.31)

И, в частности, в разрешенном виде

p2 = p:il + p2>2(p-Po), (4-32)

где Xg, Р2 - слабоменяющиеся функции энтропии s. Для воды в диапазоне до 10* ат имеем = 7, Ргг = 3000 am~.

Анализ эффективного уравнения состояния твердой фазы осложняется фактическим наличием двух систем напряжений, определяющих гидростатическое сжатие сплошного материала под воздействием порового давления в жидкости и деформацию всего скелета в целом из-за фиктивных напряжений. В связи с этим введем в рассмотрение первый 0 инвариант тензора истинных средних напряжений в твердой фазе, связанный с первым инвариантом тензора фиктивных напряжений 0 = о -f- cs[ 4- 033 соотношением (7з)0 =

= (1 - m){/a)Q + (i - m) p. Тогда уравнение (4.30) можно представить в виде

diEi Q di J l /--3-9%

dt 3 dt Oi Pl 3 dt I -m (1-m)pi

т.е. внутренняя энергия является функцией истинного среднего-давления (-1/3)0 и фиктивных напряжений £i = £i(0; of,-; Т), причем при неизменной пористости - только истинных средних напряжений.

В условиях гидростатического сжатия а[у = ббу согласно-уравнению (4.33) имеем

где Vl = i/Pi - удельный объем материала твердой фазы.

Если теперь предполонлить, что внутреннюю энергию Ei можно представить в виде суммы двух слагаемых

El = El (Pl, Si) + E{ {mi, Si), (4.35)

где E{ - удельная внутренняя энергия сплошного материала твердой фазы; Е[ - удельная внутренняя энергия пористой среды, составленной из недеформируемых (в среднем) твердых частиц, то первое из соотношений (4.34) можно представить в виде

= p;/l-f x,p,(0-0o). (4.36)

задавая для Xj, - слабоменяющихся функций энтропии (или температуры) - те же значения, что и для обычных сплошных минералов или горных пород.

Согласно второму из соотношений (4.34) и предположения (4.35) полную объемную деформацию е можно задавать в виде нелинейной функции от двух переменных: е - ф(0, б), или е = ф (р, 0). Для малых приращений деформации будет справедлива связь

Йе = ф;й0 + Ф;р. (4.37)

Среды, характеризуемые условием фа Фр, можно назвать мягкими. Ниже подробно будут рассмотрены (§ 5) линейноупругие деформации скелета насыщенной пористой среды.

Рассмотрение проводится в рамках обычных для теорий деформаций представлений. Более тонкие эффекты выявляются прп учете зависимости объ-е.мпых деформаций переупаковки от сдвига, см. [172], где содержатся ссылки па Дуп1е источ1П1Кп.